Kezdőlap


Feladat:	F.2967	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1994/április, 198 - 199. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Síkgeometriai számítások trigonometria nélkül négyszögekben, Skatulyaelv, Téglalapok, Háromszög területe, Feladat
Hivatkozás(ok):	Feladatok: 1993/május: F.2967

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először megmutatjuk, hogy egy téglalapba írt háromszög területe legfeljebb a téglalap területének a fele. Az 1. ábrán az $A$ pontból merőlegest húzunk a téglalap $a$ oldalára. Ennek a merőlegesnek a két partján keletkezett akármelyik részháromszög területe legfeljebb akkora, mint az őt tartalmazó résztéglalap területének a fele, ezért $T_{A B C} \geq \frac{a \cdot b}{2}$ . Ha az $A, B, C$ pontok közül legalább egy a téglalap belsejében van, akkor

\begin{matrix} T_{A B C} < \frac{a \cdot b}{2} . \end{matrix}

1. ábra 2. ábra 3. ábra

Osszuk fel ezután az egységnégyzetet egyik szemközti oldalpárjával párhuzamos egyenesekkel négy

\frac{1}{4}

szélességű téglalapra (2. ábra). Mivel a négyzet belsejében 9 pont van, legalább az egyik oszlopban legalább 3 pont lesz. E három pont egyike sem eshet a téglalap

\frac{1}{4}

hosszúságú oldalára, ezért a három pont olyan háromszöget alkot, amelynek területe (1) alapján

\frac{1}{8}

-nál kisebb. Ha az elmondott felosztást a másik oldalpárral párhuzamos egyenesekkel végezzük ‐ a négyzetet így ,,sorokra'' bontjuk ‐ újra találhatunk egy olyan háromszöget, amelynek területe

\frac{1}{8}

-nál kisebb. Ha az újabb háromszög nem azonos az előzővel, akkor a bizonyítással készen vagyunk.
Hátra van még az az eset, amikor a kétféle felosztással ugyanazt a ponthármast választjuk ki. A 3. ábra ilyen esetet tüntet fel. Bebizonyítjuk, hogy ekkor bármely további

D

pont az

A, B, C

közül valamelyik kettővel

\frac{1}{8}

-nál kisebb területű háromszöget alkot. Feltehető, hogy pl.

D C

D A

és

D B

félegyenesek meghatározta szögtartományban van (valamelyikkel egybe is eshet). Az

A B C D

négyszög területét a következőképpen becsüljük:

\begin{matrix} A B < \sqrt[]{{(\frac{1}{4})}^{2} + {(\frac{1}{4})}^{2}} = \frac{\sqrt[]{2}}{4} és D C < \sqrt[]{2}, \end{matrix}

ezért

T_{A B C D} < \frac{1}{2} \cdot \frac{\sqrt[]{2}}{4} \cdot \sqrt[]{2} = \frac{1}{4}

. De akkor a

D A C

vagy

D B C

háromszögek valamelyikének a területe kisebb lesz

\frac{1}{4} : 2 = \frac{1}{8}

-nál. Ezzel a feladat állítását bizonyítottuk.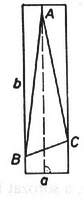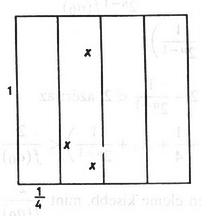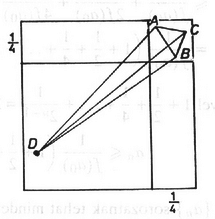