Kezdőlap


Feladat:	F.2965	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Mosonyi Milán
Füzet:	1994/január, 19 - 20. oldal		PDF \| MathML
Témakör(ök):	Egyenletek grafikus megoldása, Derékszögű háromszögek geometriája, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1993/május: F.2965

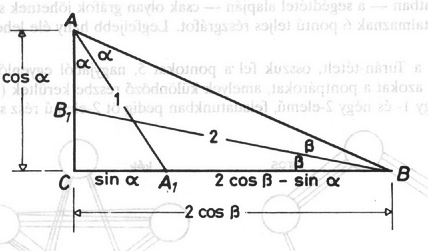
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A hegyesszögek felét jelöljük $α$ -val, illetve $β$ -val. Az 1. ábra jelöléseit használva az $A A_{1} B$ háromszögből a szinusztétel szerint

\begin{matrix} 2 \cdot cos β - sin α = \frac{sin α}{sin 2 β} . \end{matrix}

(1)

Ezzel ekvivalens a

\begin{matrix} 2 \cdot sin 2 β \cdot cos β = sin α (1 + sin 2 β) \end{matrix}

felírás, amelyből az

α + β = 45^{\circ}

összefüggéssel

\begin{matrix} 2 \cdot sin 2 β \cdot cos β = sin (45^{\circ} - β) (1 + sin 2 β) . \end{matrix}

(2)

1. ábra

Ezt az egyenletet először grafikusan próbáljuk megoldani.
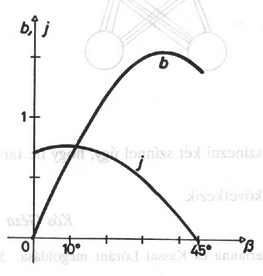
Mind a bal oldalon, mind a jobb oldalon lévő tényezők ábrázolása után ,,grafikus szorzást'' hajtunk végre. Mivel

β

csak a

(0; 45^{\circ})

intervallumban változhat, a grafikonokat elég ebben az intervallumban megrajzolni (2. ábra). A vázlatrajz egy megoldást mutat

10^{\circ}

közelében. Behelyettesítéssel megállapítható, hogy

β_{1} = 11, 5^{\circ}

esetén a bal oldal helyettesítési értéke kisebb,

β_{2} = 12^{\circ}

esetén pedig nagyobb, mint a jobb oldalé. Ezért

β_{3} = \frac{β_{1} + β_{2}}{2} = 11, 75^{\circ}

a keresett gyök egy

β_{1}

-nél és

β_{2}

-nél pontosabb közelítő értéke, és amint azt behelyettesítéssel megállapíthatjuk, a keresett gyök

β_{1}

és

β_{3}

között van. Ezt az úgynevezett felezési módszert tovább folytatva

β_{4} = \frac{β_{1} + β_{3}}{2} = 11, 625^{\circ}

közelítő értéket kapjuk

(2)

gyökére. Néhány lépés után ‐ zsebszámológéppel számolva ‐ az eléggé pontos

β = 11, 52903^{\circ}

közelítő értékhez jutunk, amellyel a bal oldal helyettesítési értéke

0, 7675235

, a jobb oldalé pedig

0, 7675226

. Ezzel a

β

értékkel

α = 33, 47097^{\circ}

, a két befogó pedig

cos α = 0, 834165

és

2 \cdot cos β = 1, 959647

2. ábra

Reményi Gusztáv

Megjegyzés. Az

(1)

egyenletből

β

-t kiküszöbölve a

\begin{matrix} tg^{3} α + tg^{2} α + (\sqrt[]{2} - 1) tg α - 1 = 0 \end{matrix}

harmadfokú egyenlethez jutunk. Az ilyen egyenletek megoldási módszere megtalálható pl. Fuchs László: Bevezetés az algebrába és számelméletbe II. rész 86. old. Az egyenletet az úgynevezett Cardano-képlettel megoldva a két befogó:

b = 0, 8341

a = 1, 9596

Mosonyi Milán (Budapest, Veres Péter Gimn., III. o. t.)