Feladat: F.2943 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Bánky Boróka ,  Csergőffy Tibor ,  Csorba Péter ,  Csörnyei Marianna ,  Dienes Péter ,  Dőtsch András ,  Futó Gábor ,  Horváth Gábor ,  Kucsera Henrik ,  Markót Mihály ,  Maróti Gábor ,  Németh Ákos ,  Péter Gábor ,  Tichler Krisztián ,  Zsenei András 
Füzet: 1993/október, 310 - 311. oldal  PDF  |  MathML 
Témakör(ök): Vetítések, Terület, felszín, Tetraéderek, Vektorok skaláris szorzata, Vektorok vektoriális szorzata, Feladat
Hivatkozás(ok):Feladatok: 1993/január: F.2943

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az AB, illetve CD élben találkozó lapok szöge derékszög. Az ábrán feltüntettük ezeknek a lapoknak az AB, illetve CD oldalakhoz tartozó magasságait. Vegyünk fel egy AB-re merőleges S síkot, és vetítsük erre merőlegesen a tetraédert. A vetületet az ábrán láthatjuk.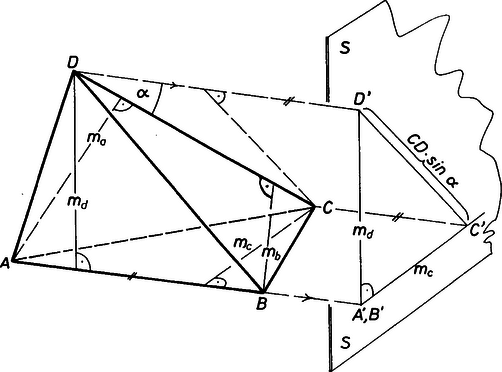

 
 

Az ABC lap vetülete egy mc, az ABD lap vetülete pedig egy md hosszúságú szakasz, amelyek a feltétel szerint derékszöget zárnak be. Ezért
mc2+md2=(C'D')2.(1)

Az S síkra való merőleges vetítésben CD vetítősíkja párhuzamos AB-vel. Ebben a vetítősíkban van a CDD'C' négyszög. Legyen ezen a síkon AB merőleges vetülete A'B'. Az ABésCD kitérő egyenesek α hajlásszöge ezen a síkon eredeti nagyságában látszik, amiért C'D'=CD⋅sinα. Ennek alapján (1)-ből mc2+md2=CD2⋅sin2α. Mindkét oldalt AB24-gyel szorozva:

(AB⋅mc2)2+(AB⋅md2)2=(AB⋅CD⋅sinα2)2.(2)

Ugyanezzel a gondolatmenettel megmutathatjuk, hogy

(CD⋅ma2)2+(CD⋅mb2)2=(AB⋅CD⋅sinα2)2.(3)

A (2) és (3) összefüggésekből következik a feladat állítása.
 

 Dőtsch András (Szeged, Ságvári E. Gyak. Gimn. III. o. t.)
 

II. megoldás. Jelöljük pl. az ABC lap területét tD-vel, a tD hosszúságú és ABC síkjára merőleges (kifelé irányított) vektort tD→-vel. Ismert tétel, hogy egy poliéder kifelé irányított lap-területvektorainak összege zérusvektor. (Lásd pl. Hajós György: Bevezetés a geometriába c. könyvének 322. oldalán.) A feladat feltételei szerint tA→ és tB→, valamint tC→ és tD→ merőlegesek, ezért a skaláris szorzatuk nulla:
tA→⋅tB→=0éstC→⋅tD→=0.(4)

Az említett tétel szerint tA→+tB→+tC→+tD→=0→, azaz tA→+tB→=-(tC→+tD→), amiből (tA→+tB→)2=(tC→+tD→)2. A négyzetre emelést elvégezve és (4)-et fölhasználva:
tA2+tB2=tC2+tD2.