Kezdőlap


Feladat:	F.2941	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Csörnyei Marianna , Dőtsch András , Horváth Gábor , K. L. , Marx Gábor , Pete Gábor
Füzet:	1993/október, 306 - 308. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1993/január: F.2941

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Írjuk a bizonyítandó egyenlőtlenséget

\begin{matrix} m ⩽ \frac{cos \frac{γ}{2}}{2 sin \frac{γ}{2}} \cdot c + \frac{c}{sin \frac{γ}{2}} - (a + b) & (1) \end{matrix}

alakba.
Először bebizonyítjuk, hogy

\begin{matrix} m ⩽ \frac{cos \frac{γ}{2}}{2 sin \frac{γ}{2}} \cdot c, & (2) \end{matrix}

majd pedig azt, hogy

\begin{matrix} \frac{c}{sin \frac{γ}{2}} ⩾ a + b . & (3) \end{matrix}

Ezekből már következik a feladat állítása.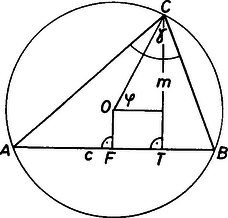

1. ábra

A (2) állítás belátásához használjuk az 1. ábrát. Az ábra jelöléseivel

m = O F + O C \cdot sin φ

, ami adott

c és γ

esetén csak

φ

-től függ, és akkor maximális, ha

φ = 90^{\circ}

. Ezért

m

akkor lesz a legnagyobb, ha átmegy a körülírt kör

O

középpontján, azaz ha háromszög egyenlő szárú. A 2. ábra alapján a maximális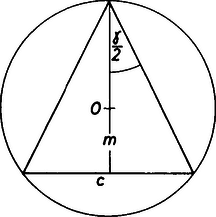

m -re tg\frac{γ}{2}=\frac{c}{2 m},

amiből

m = \frac{cos \frac{γ}{2}}{2 sin \frac{γ}{2}} \cdot c .

Ezért általában

m ⩽ \frac{cos \frac{γ}{2}}{2 sin \frac{γ}{2}} \cdot c

2. ábra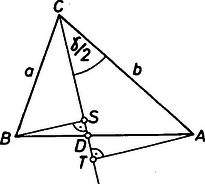

3. ábra

A (3) egyenlőtlenség igazolásához tekintsük a 3. ábrát. A

B D S

derékszögű háromszögből

B S < B D,

és ha

a = b,

akkor

B S = B D,

ezért bármely háromszög esetén

B S ⩽ B D .

Hasonlóan kaphatjuk, hogy

A T ⩽ A D .

Ezért

B S + A T ⩽ B D + A D = A B = c

. Ebből, és a

B S = a \cdot sin \frac{γ}{2},

valamint

A T = b \cdot sin \frac{γ}{2}

összefüggésekből

\begin{matrix} a \cdot sin \frac{γ}{2} + b \cdot sin \frac{γ}{2} ⩽ c, & (4) \end{matrix}

és itt egyenlőség csak egyenlő szárú háromszög esetén áll fenn. Látjuk, hogy (4) ekvivalens (3)-mal, tehát igaz a feladat állítása. Egyenlőség pontosan akkor lesz, ha

a = b

Zsenei András (Bp., ELTE Radnóti M. Gyak. Gimn., IV. o. t.)

II. megoldás. Legyen

a + b + m = k \cdot c .

a = 2 r \cdot sin α

összefüggés alapján

m = 2 r \cdot sin α \cdot sin β,

és így

\begin{matrix} k = \frac{a + b + m}{c} = \frac{2 r sin α + 2 r sin β + 2 r sin α sin β}{2 r sin γ} = \frac{sin α + sin β + sin α sin β}{sin γ} . \end{matrix}

Közismert összefüggésekkel:

\begin{matrix} k & = \frac{2 sin \frac{α + β}{2} \cdot cos \frac{α - β}{2} + \frac{cos (α - β) - cos (α + β)}{2}}{sin γ} = \\ = \frac{2 cos \frac{γ}{2} \cdot cos \frac{α - β}{2} + \frac{2 \cdot cos^{2} \frac{α - β}{2} - 1 + cos γ}{2}}{sin γ} = \\ = \frac{2 \cdot cos^{2} \frac{α - β}{2} + 4 cos \frac{γ}{2} \cdot cos \frac{α - β}{2} + cos γ - 1}{2 sin γ} . \end{matrix}

Ez a kifejezés a pozitív

cos \frac{α - β}{2}

-nek szigorúan monoton növő másodfokú függvénye. Tekintve, hogy

cos \frac{α - β}{2} ⩽ 1, k

akkor lesz legnagyobb, ha

cos \frac{α - β}{2} = 1,

azaz ha a háromszög egyenlő szárú. Így azt nyertük, hogy

\begin{matrix} k ⩽ \frac{4 \cdot cos \frac{γ}{2} + 1 + cos γ}{2 \cdot sin γ} = \frac{4 \cdot cos \frac{γ}{2} + 2 \cdot cos^{2} \frac{γ}{2}}{2 \cdot 2 \cdot sin \frac{γ}{2} \cdot cos \frac{γ}{2}} = \frac{2 + cos \frac{γ}{2}}{2 \cdot sin \frac{γ}{2}} . \end{matrix}

Tehát valóban

\begin{matrix} a + b + m ⩽ \frac{2 + cos \frac{γ}{2}}{2 \cdot sin \frac{γ}{2}} \cdot c . \end{matrix}