| Feladat: | F.2940 | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Csörnyei Marianna , K. L. | ||
| Füzet: | 1994/január, 17 - 19. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gráfok komplementere, Teljesgráfok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1993/január: F.2940 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat az 1992. évi Nemzetközi Matematikai Diákolimpia 3. feladatának (ld. KöMaL 1993/1. szám 3‐4. oldal) módosítása.
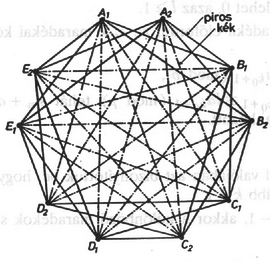
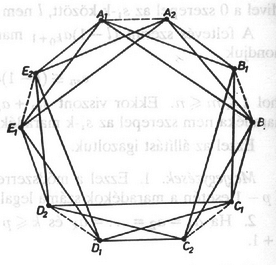
A jobb áttekinthetőség érdekében folytonos szakaszokkal ábrázoljuk a piros éleket, a kék színűeket most nem rajzoljuk be. A teljes gráfból kimaradó élt szaggatott vonal jelzi. A 2. ábráról jól látszik, hogy a gráfban nincs egyszínű háromszög. Ha a pontok közül kettőt piros él köt össze, akkor ez a két pont -val együtt egy piros háromszöget alkot. Ha pedig a háromszög élei közül egyik sem piros, akkor egy kék háromszög. 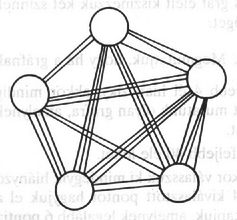 3. ábra A Turán-tétel arra ad választ, hogy legfeljebb hány éle lehet egy pontú gráfnak, ha az nem tartalmaz pontú teljes részgráfot; sőt a maximális élszámú gráfokat is leírja. Maximális élszámú gráfot úgy kapunk, hogy az csúcsot ,,nagyjából'' egyenlő részre osztjuk (azaz két tetszőleges részben a csúcsok számának különbsége legfeljebb lehet), és azokat a pontokat kötjük össze, amelyek különböző részbe kerültek. A feladatban ‐ a segédtétel alapján ‐ csak olyan gráfok jöhetnek szóba, amelyek nem tartalmaznak pontú teljes részgráfot. Legfeljebb hány éle lehet egy ilyen gráfnak? Ismerve a Turán-tételt, osszuk fel a pontokat , nagyjából egyenlő részre, és kössük össze azokat a pontpárokat, amelyek különböző részbe kerültek (az olimpiai feladatban egy - és négy -elemű, feladatunkban pedig öt -elemű rész szerepelt). Az az érdekes, hogy ezt a gráfot ki lehet színezni két színnel úgy, hogy ne tartalmazzon egyszínű háromszöget (3. ábra, 4. ábra). 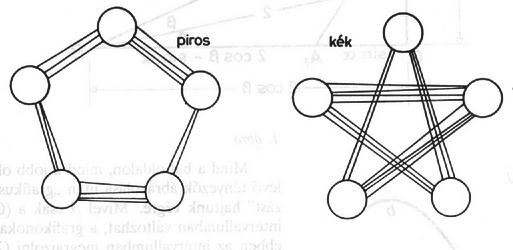 4. ábra
|