Kezdőlap


Feladat:	F.2935	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Csörnyei Marianna , Futó Gábor , Marx Gábor
Füzet:	1993/szeptember, 259 - 261. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Síkbeli szimmetrikus alakzatok, Feladat
Hivatkozás(ok):	Feladatok: 1992/december: F.2935

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Trapéz rombuszba írásán azt értjük, hogy a trapéz csúcsai a rombusz határán vannak. Ha a rombusz négyzet, akkor egyetlen maximális területű szimmetrikus trapéz írható bele, önmaga.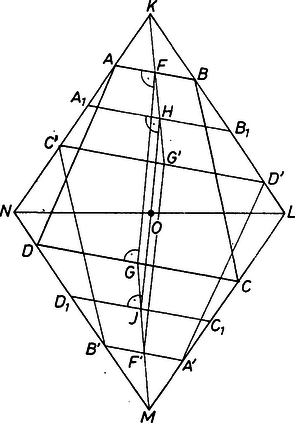

1. ábra

Az 1. ábrán a

K L M N

rombuszba beírt szimmetrikus trapézt rajzoltunk meg,

A B ∥ C D

, és tükröztük a trapézt a rombusz

O

középpontjára. Ha

A B

, illetve

C D

felezőpontja

F

, illetve

G

, akkor

K, F, G'

, továbbá

M, F', G

egy egyenesen vannak, és

\begin{matrix} G F ⊥ A B, G' F' ⊥ A' B' . (1) \end{matrix}

Tekintsük az

A B D' C'

trapéz

A_{1} B_{1}

középvonalát. Ennek

H

felezőpontja illeszkedik a

K F

egyenesre, és a

H

pont felezi az

F G'

szakaszt is. Hasonlót mondhatunk az

A' B' D C

trapéz

C_{1} D_{1}

középvonalának

J

felezőpontjáról. Könnyen beláthatjuk, hogy

\begin{matrix} A_{1} B_{1} = C_{1} D_{1} = \frac{A B + C D}{2}, (2) \end{matrix}

továbbá

H J

párhuzamos

G F

-fel, és így (1) szerint

H J ⊥ C_{1} D_{1}

és

H J ⊥ A_{1} B_{1}

. Ezért

A_{1} B_{1} C_{1} D_{1}

olyan téglalap, amelynek középpontja

O

. Azt is láthatjuk, hogy e téglalap és a trapéz magassága egyenlő,

F G = H J

, ezért (2) miatt a területük is megegyezik.
Nézzük meg ezután, hogyan szerkeszthető adott rombuszba téglalap. Mivel a rombusz és a téglalap

O

középpontja megegyezik, ezért a téglalap csúcsai

O

-tól egyenlő távolságra vannak, így illeszkednek egy

O

középpontú körre. A 2. ábrán láthatjuk, hogyan szerkeszthetők ilyen téglalapok.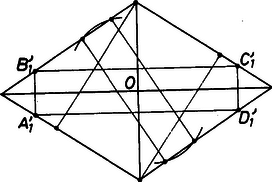

2. ábra

Az ábra

A'_{1} B'_{1} C'_{1} D'_{1}

téglalapjánál az

A'_{1} C'_{1}

átló nagyobb, mint a rombusz kisebbik átlója, a többi esetben legfeljebb akkora. Az előbbinél mindegyik rombuszoldalon egy-egy téglalap csúcs lesz, és ekkor e téglalap valamelyik két oldalával párhuzamos alapokkal rendelkező beírt szimmetrikus trapéz szimmetriatengelye az egyik rombuszátló.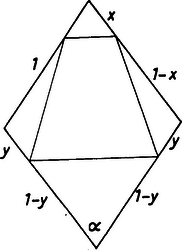

3. ábra

A 3. ábra jelöléseit használva számítsuk ki a beírt trapéz oldalai által levágott háromszögek területeinek

t

összegét:

t = [\frac{x^{2}}{2} + \frac{2 (1 - x) y}{2} + \frac{{(1 - y)}^{2}}{2}] sin α = \frac{{(x - y)}^{2} + 1}{2} sin α

. Ha

t

minimális, akkor a beírt trapéz területe maximális lesz. Ez pontosan akkor következik be, ha

x = y

. Ez azt jelenti, hogy végtelen sok ilyen típusú trapéz van, ezek területe a rombusz területének a fele.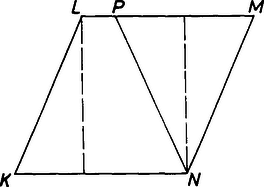

4. ábra

A 2. ábra további téglalapjai olyanok, hogy két szemközti oldaluk a rombusz két szemközti oldalára illeszkedik. Ilyen esetet rajzoltunk meg a 4. ábrán, ahol a rombusz hegyesszöge

60^{\circ}

-nál nagyobb. Az ilyen típusúak között maximális területű téglalap oldalait szaggatott vonallal rajzoltuk meg, vele egyenlő területű a

K N P L

beírt szimmetrikus trapéz, és ez a terület most nagyobb, mint a rombusz területének a fele. (Ha a rombusz hegyesszöge legfeljebb

60^{\circ}

, akkor ez a terület legfeljebb a rombusz területének a fele.)
Olyan trapéz, mint a

K N P L

, négy van, hiszen a trapéz hosszabbik alapja a rombusz bármelyik oldalával egybeeshet, és két, velük egyenlő területű beírt téglalap létezik. A 4. ábra szerinti rombuszba tehát

6

maximális területű szimmetrikus trapéz írható.
Összefoglalva: Ha

L K N ∢ \leq 60^{\circ}

, akkor a rombuszba végtelen sok maximális területű szimmetrikus trapéz írható, és a maximális terület a rombusz területének a fele. Ha

60^{\circ} < L K N ∢ < 90^{\circ}

, akkor 6 maximális területű beírt szimmetrikus trapéz lesz (ezek területe nagyobb a rombusz félterületénél), végül ha a rombusz négyzet, akkor csak egy (saját maga).

Megjegyzés. A beírást általánosabban is értelmezhettük volna, éspedig úgy, hogy a trapéz minden csúcsa a rombusznak határpontja vagy belső pontja legyen. A feladat kérdésére adandó válasz azonban ekkor is ugyanaz lesz.