Kezdőlap


Feladat:	F.2911	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csermely Zoltán , Futó Gábor , Horvai Péter , Kálmán Tamás , Párniczky Benedek , Pete Gábor
Füzet:	1993/február, 61 - 63. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Simson-egyenes, Húrnégyszögek, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1992/május: F.2911

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tekintsük a feladatot megoldottnak. A megoldást a $P$ pont helyzete szerint négy részre bontjuk.

1. Legyen

P

a konvex szögtartomány belső pontja. Húzzunk párhuzamost

P

-n át a szög száraival. Legyenek a szárakon keletkező metszéspontok

A_{1}

, illetve

B_{1}

O A_{1} = b

O B_{1} = a

, és használjuk az 1. ábra további jelöléseit is. Az

A A_{1} P

és

A O B

hasonló háromszögekből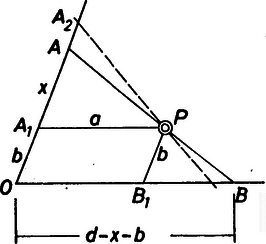

\begin{matrix} \frac{x}{a} = \frac{x + b}{d - (x + b)}, innen x^{2} - (d - a - b) x + a b = 0, \end{matrix}

vagy a

c = d - a - b

jelöléssel

x^{2} - c x + a b = 0

1. ábra

Ennek megoldása

x = \frac{c \pm \sqrt[]{c^{2} - 4 a b}}{2}

, amelyben

\sqrt[]{c^{2} - 4 a b}

ismert módon szerkeszthető, majd

x

is. A szerkesztés ezután úgy történik, hogy

O

-ból fölmérjük

b + x

-et az

O A_{1}

szárra, így kapjuk

A

-t, amelyet

P

-vel összekötve adódik a szerkesztendő egyenes. A feladat megoldható, ha

c^{2} - 4 a b \geq 0

, és

2

vagy

1

megoldás van aszerint, hogy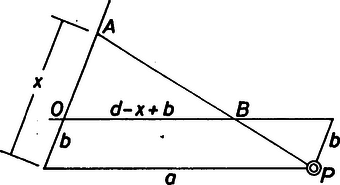

c = d - a - b > 2 \sqrt[]{a b}

vagy

d - a - b = 2 \sqrt[]{a b}

2. ábra

2. Most nézzük azt az esetet, amikor

P

a konvex szögtartomány valamelyik mellékszögének belső pontja. A 2. ábra alapján

\begin{matrix} \frac{x}{a} = \frac{x - b}{d - x + b}, ahonnan x^{2} - (d - a + b) x - a b = 0, \end{matrix}

vagy

c = d - a + b

jelöléssel:

x^{2} - c x - a b = 0, x = \frac{c \pm \sqrt[]{c^{2} + 4 a b}}{2}

; csak

x = \frac{c + \sqrt[]{c^{2} + 4 a b}}{2}

lehetséges, ezért most egy megoldás van.

3. Ha

P

a konvex szögtartomány határának egy

0

-tól különböző pontja, akkor

A

és

B

valamelyikével egybeesik. Legyen pl.

P = B

, ekkor

P O = a

és

O A = d - a

, így

A

megszerkeszthető. A megoldhatóság feltétele

d > a

, és ekkor egy megoldás lesz (3. ábra).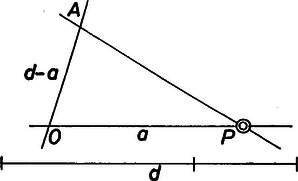

3. ábra

4. Ha

P

a konvex szögtartomány csúcsszögének határán vagy annak belsejében van, nem lesz megoldás, hiszen akkor nincs olyan

P

-n átmenő egyenes, amely a konvex szög mindkét szárát metszené.

Csermely Zoltán (Szeged, Radnóti M. Gimn.) és

Horvai Péter (Fazekas M. Főv. Gyak. Gimn.) dolgozata alapján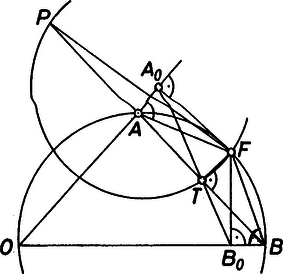

4. ábra

II. megoldás: Tekintsük most is megoldottnak a feladatot. Használjuk a 4. ábra jelöléseit. Ezen az ábrán

O A_{0} = O B_{0} = \frac{d}{2}

. Az

A_{0}

és

B_{0}

pontokban a szögszárakra állított merőlegesek metszéspontja

F

, és nyilván

A_{0} F = F B_{0}

, továbbá

\frac{d}{2} = O A + A A_{0} = O B - B B_{0}

, így

A A_{0} = B B_{0}

. Ezért az

F A_{0} A

és

F B_{0} B

derékszögű háromszögek egybevágók. Az egybevágóság következtében

A F = F B

, az

F

-ből az

A B

-re bocsátott merőleges

T

talppontja felezi az

A B

szakaszt. Egyenlőek továbbá az ábra ívvel jelölt szögei. Ez utóbbi miatt az

A O B F

négyszög húrnégyszög, tehát az

F

pont rajta van az

A O B

háromszög körülírt körén. Mivel

F

-ből az

A B O

háromszög oldalaira bocsátott merőlegesek talppontjai egy egyenesen ‐ az

F

ponthoz tartozó Simson egyenesen ‐ vannak, azért

A_{0}

T

és

B_{0}

egy egyenesre esnek. A szerkesztést ezután a következőképpen végezhetjük: Kijelöljük a szög szárain az

A_{0}

B_{0}

pontokat, majd megszerkesztjük

F

-et. A

T

pontot az

A_{0} B_{0}

egyenesből

P F

Thalész-köre metszi ki, és

P T

a szerkesztendő egyenes. Attól függően, hogy

P F

Thalész-köre hány pontban metszi az

A_{0} B_{0}

szakaszt, a feladatnak

2

1

vagy

0

megoldása lesz.