Kezdőlap


Feladat:	F.2894	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csörnyei Marianna , Futó Gábor , Újváry-Menyhárt Zoltán
Füzet:	1992/szeptember, 257 - 258. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Középpontos és egyéb hasonlósági transzformációk, Feladat
Hivatkozás(ok):	Feladatok: 1992/február: F.2894

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Húzzunk párhuzamost a háromszög csúcsain keresztül a szemközti oldalakkal.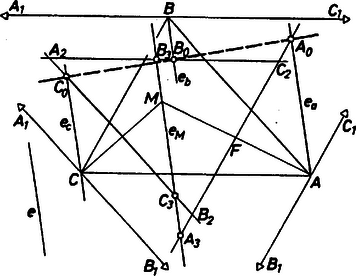

A keletkezett háromszög legyen

A_{1} B_{1} C_{1}

. Az

M

pont az

A_{1} B_{1} C_{1}

háromszög körülírt körének a középpontja. Legyen ennek a háromszögnek az

M

pontra vonatkozó,

\frac{1}{2}

arányú középpontos hasonlósággal szerkesztett képe

A_{2} B_{2} C_{2}

. Így

M

A_{2} B_{2} C_{2}

háromszög körülírt körének is középpontja. Az

\frac{1}{2}

arányú kicsinyítés révén az

A_{2} B_{2} C_{2}

háromszög oldalai az

A M

B M

C M

szakaszok felező merőlegesei. Legyenek az

A

B

C

és

M

pontokon át

e

-vel húzott párhuzamosok

e_{A}

e_{B}

e_{C}

és

e_{M}

. Az

e_{M}

egyenes messe az

A_{2} B_{2} C_{2}

háromszög oldalegyeneseit az

A_{3}

B_{3}

C_{3}

pontokban az ábra szerint. A Menelaosz-tétel alapján:

\begin{matrix} \frac{B_{2} A_{3}}{A_{3} C_{2}} \cdot \frac{C_{2} B_{3}}{B_{3} A_{2}} \cdot \frac{A_{2} C_{3}}{C_{3} B_{2}} = - 1. & (1) \end{matrix}

Mivel

F

A M

felezőpontja, az

A A_{0} F

és

M A_{3} F

háromszögek egybevágóak. Ezért

A_{0} F = F A_{3}

, és mert

F

B_{2} C_{2}

-nek is felezőpontja,

C_{2} A_{0} = A_{3} B_{2}

. Így

\begin{matrix} \frac{B_{2} A_{3}}{A_{3} C_{2}} & = \frac{A_{0} C_{2}}{B_{2} A_{0}} . & Ugyanígy megmutatható, hogy & (2) \\ \frac{C_{2} B_{3}}{B_{3} A_{2}} & = \frac{B_{0} A_{2}}{C_{2} B_{0}} & és \frac{A_{2} C_{3}}{C_{3} B_{2}} = \frac{C_{0} B_{2}}{A_{2} C_{0}} . & (3) \end{matrix}

Vegyük (1) mindkét oldalának reciprokát, és helyettesítsük az így kapott egyenletbe a (2) és (3) jobb oldalán lévő értékeket:

\begin{matrix} \frac{B_{2} A_{0}}{A_{0} C_{2}} \cdot \frac{C_{2} B_{0}}{B_{0} A_{2}} \cdot \frac{A_{2} C_{0}}{C_{0} B_{2}} = - 1. \end{matrix}

(4)

A (4) formula az

A_{2} B_{2} C_{2}

háromszögben a Menelaosz-tétel megfordítása szerint éppen azt jelenti, hogy az

A_{0}

B_{0}

C_{0}

pontok egy egyenesre illeszkednek.

Ujváry-Menyhárt Zoltán (Fazekas M. Főv. Gyak. Gimn., IV. o. t.) dolgozata alapján