Feladat: F.2877 Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Csörnyei Marianna ,  Faragó Gergely ,  Futó Gábor 
Füzet: 1992/október, 294 - 295. oldal  PDF  |  MathML 
Témakör(ök): Egész számok összege, Kombinatorikus geometria síkban, Téglalapok, Teljes indukció módszere, Feladat
Hivatkozás(ok):Feladatok: 1991/november: F.2877

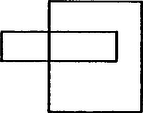
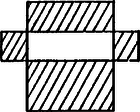
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy téglalap két részre osztja a síkot. Az a célunk, hogy a második (és minden további) téglalapot úgy vegyük föl, hogy a keletkezett síkrészek száma a lehető legtöbb legyen. Az 1. és 2 ábra szerinti felvétellel a síkrészek száma 2-vel, illetve 3-mal nőtt. Könnyen láthatjuk, hogy az új síkrészek száma akkor lesz a legnagyobb, ha a második téglalap kerülete négy pontban metszi az első téglalap kerületét. Ekkor ugyanis a négy metszéspont meghatározta téglalap mindegyik oldala fölött keletkezik egy-egy új síkrész, amelyeket a 3. ábrán bevonalkáztunk.

 

 
1. ábra
 
2. ábra
 
3. ábra

Két téglalap tehát maximálisan 2 + 4 részre osztja a síkot. Az előbbi meggondolást alkalmazva, a harmadik téglalap mindkét már fölvett téglalapot 4 ‐ 4 pontban metszve legfeljebb 4⋅2 új síkrészt hozhat létre, ezért három téglalap legfeljebb 2+4⋅1+4⋅2 részre osztja a síkot. Azt sejtjük, hogy n téglalap legfeljebb Sn=2+4⋅1+4⋅2+...+4(n-1) részre osztja a síkot. Sn a következőképpen írható: Sn=2+4(1+2+...+n-1)=2+4⋅n(n-1)2, s így Sn=2n2-2n+2, amit teljes indukcióval igazolhatunk.
n=1-re S1=2, tehát igaz az állítás. Tegyük fel, hogy ez a képlet n-re igaz. Az (n+1)-edik téglalap az előbbiek mindegyikét 4 pontban metszve 4⋅n metszéspontot hoz létre, s így legfeljebb 4⋅n új síkrész keletkezik. Ezért Sn+1=2n2-2n+2+4n=2(n+1)2-2(n+1)+2, tehát az állítás n+1-re is teljesül.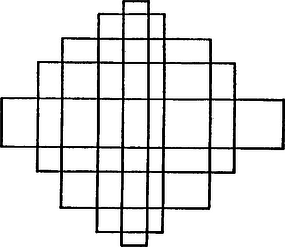
 
 

4. ábra
 

Megoldásunk azt is mutatja, hogyan oszthatjuk maximális számú részre a síkot n párhuzamos oldalú téglalappal. A 4. ábrán megrajzoltuk az n=5-nek megfelelő esetet.