Kezdőlap


Feladat:	F.2876	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Barát János , Csorba Péter , Csörnyei Marianna , Dőtsch András , Futó Gábor , Gefferth András , Kis Gábor , Pál Ambrus , Párniczky Benedek , Pete Gábor , Ratkó Éva , Szeidl Ádám
Füzet:	1992/szeptember, 254 - 255. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Négyszögek geometriája, Vektorok lineáris kombinációi, Feladat
Hivatkozás(ok):	Feladatok: 1991/november: F.2876

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I.megoldás. Jelöljük a $P Q$ szakasz felezőpontját $R$ -rel. Megmutatjuk, hogy az $\vec{R E}$ vektor egyállású az $\vec{E F}$ vektorral, amiből már következik, hogy az $R, E, F$ pontok egy egyenesen vannak.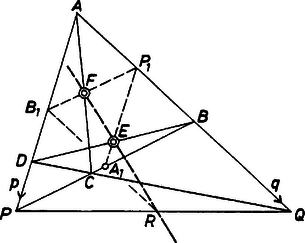

Legyen

\vec{A P} = p, \vec{A Q} = q, és így \vec{A D} = α \cdot p, \vec{A B} = β \cdot q (0 < α, β < 1)

.
Ezekből

\vec{A R} = \frac{p + q}{2} és \vec{A E} = \frac{α p + β q}{2}

. Írjuk föl kétféleképpen az

\vec{A C}

vektort.

\begin{matrix} \vec{A C} = \vec{A D} + γ \vec{D Q} = α p + γ (q - α p) = (α - α γ) p + γ q, \\ \vec{A C} = \vec{A B} + δ \vec{B P} = β q + δ (p - β q) = δ p + (β - β δ) q, \end{matrix}

ahol

γ és δ

valós számok. A kétféle fölírást összehasonlítva:

α - α γ = δ

és

γ = β - β δ

. Ebből az egyenletrendszerből

γ = β \frac{1 - α}{1 - α β}

és

δ = α \frac{1 - β}{1 - α β}

. A kapott értékekkel

\vec{A C} = (α - α β \frac{1 - α}{1 - α β})

+ (β - α β \frac{1 - β}{1 - α β})

q. Mivel

\vec{A F} =

\frac{1}{2} \vec{A C}

\vec{E F}

így határozható meg:

\vec{E F} = \vec{A F} - \vec{A E} = \frac{1}{2} α β (\frac{α - 1}{1 - α β} p + \frac{β - 1}{1 - α β} \cdot q) = \frac{α β}{2 (1 - α β)} [(α - 1) p + (β - 1) q]

. Végül

\vec{R E} = \vec{A E}

- \vec{A R} =

\frac{1}{2} [(α - 1)

+ (β - 1) q]

, és így

\frac{α β}{1 - α β}

\cdot \vec{R E} =

\vec{E F}

, ami azt jelenti, hogy az

E F

egyenes átmegy a

P Q

szakasz

R

felezőpontján.

Szeidl Ádám (Miskolc, Földes F. Gimn., II. o. t.) dolgozata alapján

II.megoldás. Jelöljük az

A B, B P, P A

szakaszok felezőpontját rendre

P_{1}, A_{1},

illetve

B_{1}

-gyel. Mivel

A_{1} P_{1}

középvonal az

A B P

háromszögben,

E

illeszkedik

A_{1} P_{1}

-re. Hasonló okból

F

illeszkedik

B_{1} P_{1}

-re,

R

pedig

A_{1} B_{1}

-re. A Menelaosz-tétel megfordítása szerint az

A_{1} B_{1} P_{1}

háromszög oldalain fekvő

F, E, R

pontok éppen akkor lesznek egy egyenesen, ha teljesül az

\begin{matrix} \frac{A_{1} E}{E P_{1}} \cdot \frac{P_{1} F}{F B_{1}} \cdot \frac{B_{1} R}{R A_{1}} = - 1 & (1) \end{matrix}

egyenlőség; ezt kell tehát megmutatnunk. A háromszög középvonalára vonatkozó tétel szerint

A_{1} E = \frac{1}{2} P D

E P_{1} = \frac{1}{2} D A

P_{1} F = \frac{1}{2} B C

F B_{1} = \frac{1}{2} C P

B_{1} R = \frac{1}{2} A Q

R A_{1} = \frac{1}{2} Q B

. Ezeket fölhasználva (1) a következő alakot ölti:

\begin{matrix} \frac{P D}{D A} \cdot \frac{B C}{C P} \cdot \frac{A Q}{Q B} = - 1. \end{matrix}

Ez pedig igaz, hiszen nem más, mint az

A B P

háromszögre és a

Q, C, D

pontokon átmenő egyenesre alkalmazott Menelaosz-tétel.

Kis 729 Gábor (Debrecen, Fazekas M. Gimn. III. o. t.) dolgozata alapján

III. megoldás. Feladatunk állítását H. S. M. Coxeter ‐ S. L. Greitzer szerzők Az újra felfedezett geometria c. könyvének 92. oldalán lévő 3.1.4. és 91. oldalán lévő 3.1.3. tételek segítségével is megmutathatjuk. A 3.1.4. tétel szerint az

E F P

és

E F Q

háromszögek területe egyenlő, ugyanis e tétel alapján mindkét háromszög területe az

A B C D

négyszög területének a negyede. Ezért az

E F

átló felezi az

E Q F P

négyszög területét. A 3.1.3. tétel szerint, ha egy átló a négyszöget két egyenlő területű részre osztja, akkor ez az átló felezi a másik átlót. Ezt a tételt az

E Q F P

négyszögre alkalmazva azt kapjuk, hogy

E F

felezi a

P Q

szakaszt.

Dőtsch András (Szeged, Ságvári E. Gyak. Gimn. II. o. t.) dolgozata nyomán