Kezdőlap


Feladat:	F.2870	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bagyinszki Róbert , Barcsi Péter , Csoma Roland , Csörnyei Marianna , Dőtsch András , Faragó Gergely , Futó Gábor , Győrffy Werner , Győry Máté , Kálmán Tamás , Megyesi Zoltán , Molnár-Sáska Gábor , Németh Ákos , Ratkó Éva
Füzet:	1992/április, 154 - 156. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Magasságvonal, Szögfelező egyenes, Körülírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1991/október: F.2870

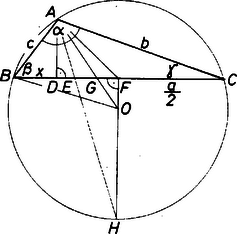
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $O$ a körülírt kör középpontja, $G$ pedig $A O$ és $B C$ metszéspontja. Használjuk az ábra további jelöléseit is. Feltehetjük, hogy $A B < A C$ . (Az $A B = A C$ esetben a feladat állítása nem érdekes.)

I. megoldás. A kerületi és középponti szögek tétele szerint

A O B ∢ = 2 γ

, ezért

B A O ∢ = 90^{\circ} - γ

. Könnyen látható, hogy

B A D ∢ = 90^{\circ} - β

és

B A E ∢ = \frac{α}{2} = 90^{\circ} - \frac{β + γ}{2} .

Feltevésünk szerint

A B < A C

, ezért

β > γ

, így az előbb kiszámított szögekre:

\begin{matrix} B A D ∢ < B A E ∢ < B A O ∢ . \end{matrix}

Ennek alapján a pontok sorrendje a

B C

oldalon:

B, D, E, F, C

. Mivel a háromszög tompaszögű,

O

a háromszögön kívül van. Ezért

E G < E F

, és így elég azt megmutatni, hogy

D E < E G

. Számítsuk ki a

D E A

és

E A G

szögeket. Ezeket a korábban már meghatározott szögek különbségeként kaphatjuk:

\begin{matrix} D A E ∢ = E A G ∢ = \frac{β - γ}{2} . \end{matrix}

Ez azt jelenti, hogy az

A D G

derékszögű háromszögben

A E

szögfelező. Mivel

A D < A G

, a szögfelező osztási arányára vonatkozó tételből láthatjuk, hogy

D E < E G

, amiből már következik a feladat állítása.

Megjegyzés. A megoldásból látható, hogy az

A

csúcsnál lévő szög nagyságától függetlenül érvényes a következő tétel: A háromszög bármelyik magasságvonalának a vele egy csúcsból induló szögfelezőre vonatkozó tükörképe átmegy a körülírt kör középpontján.

II. megoldás. Ismeretes, hogy a

B C

oldal felező merőlegese és az

A

csúcsból húzott belső szögfelező a körülírt körön metszik egymást. Az

A D E

és

H F E

háromszögek hasonlóak. Világos, hogy

A D < H F

, hiszen

A D

kisebb, mint egy, a

H O

átmérőegyenessel párhuzamos húr fele,

H F

pedig nagyobb, mint egy átmérő fele. De ha

A D < H F

, akkor az előbbi hasonlóság következtében

D E < E F

III. megoldás. Kifejezzük

D E

-t és

E F

-et a háromszög oldalaival, és összehasonlítjuk a két szakaszt. A szögfelezőre vonatkozó tétel szerint

\begin{matrix} \frac{c}{b} = \frac{B E}{a - B E}, amiből B E = \frac{a \cdot c}{b + c} . \end{matrix}

A Pitagorasz tétel alapján

c^{2} = x^{2} + A D^{2} és b^{2} = {(a - x)}^{2} + A D^{2}

, ezekből

x = \frac{a^{2} + c^{2} - b^{2}}{2 a}

. Most már kiszámíthatjuk

D E

-t:

\begin{matrix} D E = B E - B D = \frac{a \cdot c}{b + c} - \frac{a^{2} + c^{2} - b^{2}}{2 a} = \frac{b - c}{2 a (b + c)} [{(b + c)}^{2} - a^{2}], \end{matrix}

ahol fölhasználtuk, hogy

b > c

, és ezért a pontok sorrendje a

B C

oldalon

B, D, E, F, C

. Hasonló meggondolással

E F = B F - B E = \frac{a}{2} - \frac{a \cdot c}{b + c} = \frac{b - c}{2 (b + c)} \cdot a

. A feladat állítása azt jelenti, hogy

\begin{matrix} \frac{b - c}{2 a (b + c)} [{(b + c)}^{2} - a^{2}] < \frac{b - c}{2 (b + c)} \cdot a, azaz \\ \frac{{(b + c)}^{2} - a^{2}}{a} < a, másképpen {(b + c)}^{2} < 2 a^{2} . \end{matrix}

Elegendő tehát a legutóbb kapott egyenlőtlenséget igazolni. A koszinusztétel szerint

a^{2} = b^{2} + c^{2} - 2 b c \cdot cos α

, amiből

a^{2} > b^{2} + c^{2}

, hiszen

cos α < 0

. Mivel

{(b - c)}^{2} > 0

, így

b^{2} + c^{2} > 2 b c

; tehát az előbbi egyenlőtlenségből:

\begin{matrix} 2 a^{2} > 2 b^{2} + 2 c^{2} > b^{2} + c^{2} + 2 b c = {(b + c)}^{2} . \end{matrix}

Megjegyzések. 1. Könnyen belátható, hogy a

D E \geq E F

esetben a háromszög csak hegyesszögű lehet. Ekkor ugyanis

2 a^{2} \leq {(b + c)}^{2}

teljesül, amit a koszinusztétel felhasználásával átalakítva:

\begin{matrix} 2 (b^{2} + c^{2} - 2 b c \cdot c o s α) \leq b^{2} + c^{2} + 2 b c, innen \\ cos α \geq \frac{{(b - c)}^{2}}{4 b c}, tehát a háromszög hegyesszögű . \end{matrix}

2. A feladat állítása kiterjeszthető. A II. megoldásból azonnal látszik, hogy

D E < E F

akkor is teljesül, ha az

A

csúcsnál derékszög van.