Feladat: F.2864 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Csorba Péter ,  Futó Gábor ,  Gefferth András ,  Hajba Tamás ,  Kálmán Tamás ,  Kis Gábor ,  Lente Gábor ,  Párniczky Benedek 
Füzet: 1992/március, 111 - 112. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Beírt kör, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):Feladatok: 1991/szeptember: F.2864

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I.megoldás. Használjuk az ábra jelöléseit. Legyen az ABC háromszög kerülete 2s, a c oldallal párhuzamos érintőszakasz pedig x=A1B1 . A beírt kör az AC, illetve a BC oldalt az A2, illetve a B2 pontban érinti.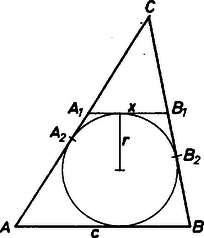

 
 

Az ABC és A1B1C háromszögek nyilván hasonlóak, a hasonlóság aránya legyen k. Az A1,B1 és A,B pontokból a beírt körhöz húzott érintőszakaszok egyenlősége révén    x=A1B1=A1A2+B1B2=k⋅c és AA2+BB2=c. Ezért az ABC háromszög kerülete:
2s=2c+CA1+x+CB1=2c+k⋅2s

Ebből s=c+k⋅s, amit k-val szorozva: k⋅s=k⋅c+k2⋅s;k⋅c=x-et kifejezve:
x=s⋅(k-k2).
A k↦k-k2 függvény legnagyobb értéke a k=12 helyen van, és a maximuma 14. Ezért x legnagyobb értéke s4 lehet, ami valóban a kerület nyolcadrésze. Ez meg is valósul, ha k⋅c=s4, azaz c=s2.
 
II. megoldás. Jelöljük a beírt kör sugarát r-rel, a c oldalhoz tartozó magasságot pedig m-mel. Az első megoldásban említett hasonlóság alapján xc=m-2rm=1-2rm.
A háromszög területe kifejezhető a beírt kör sugarával: c⋅m2=r⋅s, amiből 2rm=cs. Az így kapott két összefüggésből xc=1-cs, vagyis x⋅s=c(s-c). A számtani és mértani közép közötti egyenlőtlenség szerint c(s-c)≤(c+s-c2)2=s24, ezért x⋅s≤s24, és így x≤s4, amint azt állítottuk. Egyenlőség pontosan akkor lesz, ha c=s-c, azaz c=s2 esetén. Szavakban: akkor, ha a háromszög egyik oldala éppen a kerület negyedrésze, egyben az ehhez tartozó magasság 4r. Ilyen oldal legfeljebb egy lehet.
 

 Futó Gábor (Fazekas M. Főv. Gyak. Gimn., II. o. t.)