Kezdőlap


Feladat:	F.2858	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csekő Zoltán , Csörnyei Marianna , Párniczky Benedek , Stőhr Lóránt , Varjú Katalin
Füzet:	1992/április, 152 - 154. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Hozzáírt körök, Hossz, kerület, Terület, felszín, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1991/május: F.2858

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. Felidézünk néhány összefüggést a háromszög beírt és hozzáírt köreinek érintőszakaszai és a kerület bizonyos részei között. Ismeretes, hogy az $A B C$ háromszög beírt körének érintési pontjai közül kettő pl. az $A$ csúcstól $s - a$ távolságra van. Ezért az 1. ábra jelölései szerint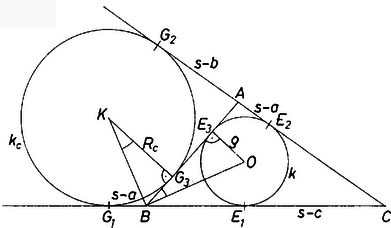

1. ábra

\begin{matrix} A E_{2} = A E_{3} = s - a; B E_{1} = B E_{3} = s - b; C E_{1} = C E_{2} = s - c . \end{matrix}

(1)

Hasonlóan a

c

oldalhoz hozzáírt kör érintési pontjaira:

\begin{matrix} A G_{2} = A G_{3} = s - b; B G_{1} = B G_{3} = s - a; C G_{1} = C G_{2} = s . \end{matrix}

(2)

Az 1. ábrán egy ívvel jelölt merőleges szárú szögpárok révén az

O B E_{3}

és

B K G_{3}

háromszögek hasonlóak, ezért

\frac{R_{c}}{s - a} = \frac{s - b}{ϱ}

, amiből

R_{c} = \frac{(s - a) (s - b)}{ϱ}

. A Heron-, illetve a

t = ϱ \cdot s

képlet felhasználásával

\begin{matrix} R_{c} = \frac{t}{s - c} . \end{matrix}

(3)

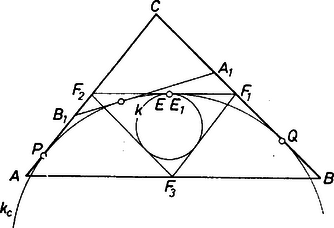2. ábra

2. Az (1)‐(3) képleteinket értelemszerűen alkalmazzuk a vizsgált háromszögekre, a továbbiakban

2 s

ezeknek a kerületét jelentse; vagyis az eddiginek a felét.
Az

A B C

háromszög oldalainak

F_{,} F_{2}, F_{3}

felezőpontjai nyilván teljesítik a feladat feltételeit (2.ábra). Ha

A_{1}, B_{1}, C_{1}

is ilyen pontok, akkor mind a

C F_{2} F_{1}

, mind pedig a

C B_{1} A_{1}

háromszög kerülete

2 s

. Segítségül vesszük az

F_{1} F_{2} F_{3}

háromszög beírt

k

körét és a

C F_{2} F_{1}

háromszög

F_{2} F_{1}

oldalához hozzáírt

k_{c}

kört. Figyelembe véve

(2)

harmadik egyenlőségét, e két háromszög

C

-vel szemközti oldalát érintő hozzáírt kör ugyanazokban a pontokban érinti a

C

-n átmenő oldalak egyenesét ‐ éspedig azokban a

P

és

Q

pontokban, amelyekre

C P = C Q = s

‐ ezért e két említett kör azonos. Az (1) egyenlőségek szerint

E_{1} F_{1} = s - F_{2} F_{3}

, ahol

E_{1}

F_{1} F_{2} F_{3}

háromszög beírt körének érintési pontja, (2) szerint pedig

E F_{1} = s - C F_{1}

, ahol

E

C F_{2} F_{1}

háromszög hozzáírt körének érintési pontja. Mivel

C F_{1} = F_{2} F_{3}

, azért

E_{1} = E

. Ez azt jelenti, hogy a

k

és

k_{c}

körök ugyanabban az

E

pontban érintik az

F_{1} F_{2}

szakaszt, és a

k

k_{c}

belsejében van. Ezért az

A_{1} B_{1}

szakasznak nem lehet

k

-val közös pontja, hiszen

A_{1} B_{1}

érinti a

k_{c}

kört. (Kivéve, ha

A_{1}

és

B_{1}

egybeesik az

F_{1}

és

F_{2}

pontokkal.) Azt is látjuk, hogy a

k

kör az

A_{1} B_{1}

egyenes másik partján van, mint a

C

pont. Hasonló elmondható a

B_{1} C_{1}

és

C_{1} A_{1}

szakaszokra is, tehát az

A_{1} B_{1} C_{1}

háromszög tartalmazza a

k

kört, anélkül, hogy oldalainak

k

-val közös pontja lenne. Pontosabban szólva, ha az

A_{1}, B_{1}, C_{1}

pontok között van olyan, amelyik nem esik egybe az

F_{1}, F_{2}, F_{3}

valamelyikével, akkor az

A_{1} B_{1} C_{1}

háromszögnek van olyan oldala, amelyiknek nincs közös pontja a

k

körrel. Ezért ennek a háromszögnek a beírt köre

k

-énál nagyobb sugarú, és a

t = ϱ \cdot s

formulából következően területe nagyobb, mint az

F_{1} F_{2} F_{3}

háromszög területe.

3. Jelöljük az

A B_{1} C_{1}, A_{1} B C_{1}, A_{1} B_{1} C

, illetve

F_{1} F_{2} F_{3}

háromszög területét rendre

t_{A}, t_{B}, t_{C},

illetve

t_{F}

-fel. Mivel a

C A_{1} B_{1}

és a

C F_{2} F_{1}

háromszög

C

-vel szemközti oldalához tartozó hozzáírt kör azonos, (3) alapján

\begin{matrix} \frac{t_{C}}{s - A_{1} B_{1}} = \frac{t_{F}}{s - F_{1} F_{2}}, így t_{C} = t_{F} \cdot \frac{s - A_{1} B_{1}}{s - F_{1} F_{2}} . \end{matrix}

Hasonlóan felírva

t_{A}

-t és

t_{B}

-t, majd a három egyenlőséget összeszorozva:

\begin{matrix} t_{A} \cdot t_{B} \cdot t_{C} = t_{F}^{3} \frac{(s - A_{1} B_{1}) (s - A_{1} C_{1}) (s - B_{1} C_{1})}{(s - F_{1} F_{2}) (s - F_{1} F_{3}) (s - F_{2} F_{3})} . \end{matrix}

A jobb oldalon a törtet

s

-sel bővítve és a Heron képletet alkalmazva kapjuk:

\begin{matrix} t_{A} \cdot t_{B} \cdot t_{C} = t_{F}^{3} \cdot \frac{t^{2}}{t_{F}^{2}}, aholtazA_{1} B_{1} C_{1}háromszög területét jelöli. \end{matrix}

(4)

Korábbi eredményünk szerint

t > t_{F}

, és így (4)-ből

\begin{matrix} t_{A} \cdot t_{B} \cdot t_{C} > t_{F}^{3} . \end{matrix}

(5)

Könnyű belátni, hogy

t_{A} + t_{B} + t_{C} + t = 4 t_{F}

, tehát

\begin{matrix} t_{A} + t_{B} + t_{C} < 3 t_{F} . \end{matrix}

(6)

A számtani és mértani közép közötti egyenlőtlenség alapján

\begin{matrix} t_{A} \cdot t_{B} \cdot t_{C} \leq {(\frac{t_{A} + t_{B} + t_{C}}{3})}^{3}, amit (6)-tal egybevetve \\ t_{A} \cdot t_{B} \cdot t_{C} < t_{F}^{3} . & (7) \end{matrix}

Az (5) és (7) egyenlőtlenségek egymásnak ellentmondóak. Ez azt jelenti, hogy az

F_{1}, F_{2}, F_{3}

pontokon kívül nincs olyan ponthármas, amely kielégítené a feladat feltételeit.

Párniczky Benedek (Fazekas M. Főv. Gyak. Gimn., II. o. t.) dolgozata alapján

Megjegyzés. A feladat állítása következménye az N. D. Kazarinoff: Geometriai egyenlőtlenségek c. könyv 198. oldalán található tételnek. (Ez a tétel azt mondja ki, hogy a négy háromszög közül nem az

A_{1} B_{1} C_{1}

kerülete a legkisebb.)