Kezdőlap


Feladat:	F.2846	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Álmos Attila , Csörnyei Marianna , Futó Gábor , Hajnal József , Imreh Csanád , Kórász Tamás , Lente Gábor , Maier Norbert-Zsombor , Párniczky Benedek , Pór Attila , Stőhr Lóránt , Szalkai Ákos , Tóth Csaba , Újváry-Menyhárt Zoltán
Füzet:	1992/január, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Beírt kör, Magasságpont, Terület, felszín, Nevezetes egyenlőtlenségek, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1991/március: F.2846

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat megoldásához fölhasználjuk a következő segédtételt: $Ha a_{1} \leq a_{2} \leq a_{3}$ és $b_{1} \leq b_{2} \leq b_{3},$ akkor

\begin{matrix} (a_{1} + a_{2} + a_{3}) (b_{1} + b_{2} + b_{3}) \leq 3 (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) . \end{matrix}

(1)

Ennek bizonyításához elegendő a következő négy helyes egyenlőtlenséget összeadni:

\begin{matrix} 0 \leq (a_{3} - a_{2}) (b_{3} - b_{2}), 0 \leq (a_{3} - a_{1}) (b_{3} - b_{1}), 0 \leq (a_{2} - a_{1}) (b_{2} - b_{1}) \end{matrix}

és

\begin{matrix} a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} \leq a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3} . \end{matrix}

Jelöljük a háromszög

A, B, C

csúcsával szemközti oldalt rendre

a, b, c

-vel, a háromszög területét pedig

t

-vel. Az ismert

t = r \cdot s

területképlet alapján a bizonyítandó állítást így írhatjuk: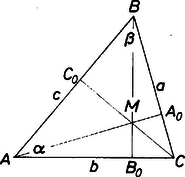

\begin{matrix} A_{0} M + B_{0} M + C_{0} M \leq \frac{3 t}{\frac{a + b + c}{2}}, \end{matrix}

amiből

\begin{matrix} (a + b + c) (A_{0} M + B_{0} M + C_{0} M) \leq 6 t . \end{matrix}

Az ábra alapján látható, hogy a háromszög kétszeres területe

2 t = a \cdot A_{0} M + b \cdot B_{0} M + c \cdot C_{0} M,

ezért a bizonyítandó egyenlőtlenség ekvivalens a következővel:

\begin{matrix} (a + b + c) (A_{0} M + B_{0} M + C_{0} M) \leq 3 (a \cdot A_{0} M + b \cdot B_{0} M + c \cdot C_{0} M) . \end{matrix}

(2)

Az oldalak jelölését megválaszthatjuk úgy, hogy

a \leq b \leq c

legyen. Ekkor például az

a

oldallal szemközti

α

és a

b

oldallal szemközti

β

szögre

α \leq β,

de így a

C

csúcsnál keletkező

A_{0} C M ∢ = 90^{\circ} - β

és

B_{0} C M ∢ = 90^{\circ} - α

szögekre

A_{0} C M ∢ \leq B_{0} C M ∢ .

Tekintve, hogy az

A_{0} C M

és

B_{0} C M

derékszögű háromszögek átfogója közös, az előbbi reláció azt is jelenti, hogy

A_{0} M \leq B_{0} M .

Hasonlóan igaz, hogy

B_{0} M \leq C_{0} M .

Ezután a (2) egyenlőtlenséget (1) mintájára beláthatjuk, hiszen (2) ugyanolyan szerkezetű reláció, mint (1), és teljesülnek az

a \leq b \leq c

és

A_{0} M \leq B_{0} M \leq C_{0} M

feltételek.

Pór Attila (Budapest, Fazekas M. Gyak. Gimn., III. o. t.)