Kezdőlap


Feladat:	F.2832	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Erben Péter , Imreh Csanád , Pór Attila , Reiff Ádám
Füzet:	1991/október, 308 - 310. oldal		PDF \| MathML
Témakör(ök):	Indirekt bizonyítási mód, Négyzetrács geometriája, Teljes indukció módszere, Szöveges feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1991/január: F.2832

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatot nyilván úgy is lehet értelmezni, hogy ha mi előre kijelöljük a megmérgezendő pontokat, akkor a bolha az irányait meg tudja-e úgy választani, hogy mérgezett pontra ne lépjen. Megmutatjuk, hogy ezt mindig meg tudja tenni.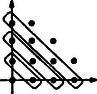

1. ábra

Legyen

R_{n}

azoknak az

(x, y)

rácspontoknak a halmaza, amelyekre

x + y = n

(1. ábra). A bolha nyilván az

n

-edik lépésben ugrik az

n + 1

darab

R_{n}

-beli pont valamelyikére.
Legyen

m_{n}

azoknak az

R_{n}

-beli pontoknak a száma, amelyeket legkésőbb az

n

-edik lépésben (tehát a bolha "megérkezéséig'') megmérgezünk. Mivel az első

n

lépésben

n

pontot mérgezünk meg, nyilván

m_{1} + m_{2} + ... + m_{n} ≦ n

2. ábra

Végül jelölje

h_{n}

azoknak az

R_{n}

-beli pontoknak a számát, ahová a bolha eljuthat. Ez nem feltétlenül azonos a meg nem mérgezett pontok számával, lehet, hogy egy pontba pl. azért nem juthat el, mert annak megmérgeztük a bal oldali és az alsó szomszédját (2. ábra). Azt fogjuk megmutatni, hogy

\begin{matrix} h_{n} ≧ n + 1 - (m_{1} + m_{2} + ... + m_{n}) . \end{matrix}

Mivel

m_{1} + ... + m_{n} ≦ n

, ebből

h_{n} ≧ 1

következik, vagyis az

n

-edik lépésben még nem lehetünk biztosak afelől, hogy a bolhát elpusztítottuk (és ez minden

n

-re igaz).

Állításunkat teljes indukcióval igazoljuk;

n = 1

-re igaz: ha

m_{1} = 0

, akkor mind a két

R_{1}

-beli pontra ugorhat a bolha; ha

m_{1} = 1

, akkor pedig az egyikre ugorhat.

Mindkét esetben

h_{1} = 2 - m_{1}

Tegyük most fel, hogy

h_{n} ≧ n + 1 - (m_{1} + ... + m_{n})

. Megmutatjuk, hogy ekkor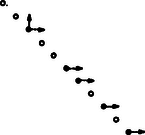

h_{n + 1} ≧ n + 2 - (m_{1} + ... + m_{n + 1})

3. ábra

A bolha

h_{n}

darab

R_{n}

-beli pontra ugorhat; ezeknek összesen legalább

1 + h_{n}

jobb oldali vagy felső szomszédja van, mert jobb oldali szomszédaik, valamint a legfelső pont felső szomszédja (ez összesen

1 + h_{n}

pont) különbözők (3. ábra). A szóba jövő

1 + h_{n}

darab

R_{n + 1}

-beli pont közül legfeljebb

m_{n + 1}

a mérgezett; a bolha tehát legalább

1 + h_{n} - m_{n + 1}

helyre ugorhat tovább úgy, hogy nem lép mérgezett pontra.

Ezzel azt kaptuk, hogy

\begin{matrix} h_{n + 1} ≧ h_{n + 1} - m_{n + 1} ≧ 1 + (n + 1 - (m_{1} + ... + m_{n})) - m_{n + 1} = n + 2 - (m_{1} + ... + m_{n + 1}) . \end{matrix}

Ezzel az állításunkat igazoltuk; semmilyen

n

-re nem tudjuk garantálni, hogy a bolhát legfeljebb

n

lépésben elpusztíthatjuk.

Megjegyzés. Ha az volna a kérdés, hogy el tudjuk-e pusztítani a bolhát véges sok lépésben, akkor arra is tagadó lenne a válasz.
(A különbség lényeges: ha pl. valaki gondol egy pozitív egész számot, azt ki lehet találni véges sok lépésben úgy, hogy végig kérdezzük az összes számot; azt azonban semmiképpen sem tudjuk vállalni, hogy pl. legfeljebb 100 találgatással kitaláljuk.)

Nevezzünk egy rácspontot "jó''-nak, ha a bolha arra lépve még akármilyen sokáig életben tud maradni. A feladat megoldásából az derült ki, hogy az origó "jó'' rácspont.

Bebizonyítjuk, hogy, "jó'' rácspontról a bolha tovább tud ugrani egy újabb "jó'' rácspontra.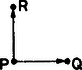

4. ábra

Legyen

P

egy " jó'' rácspont, a jobb és felső szomszédai legyenek

Q

és

R

( 4. ábra). Tegyük fel, hogy

Q

és

R

egyike sem " jó''. Ekkor léteznek olyan

n

és

k

pozitív egészek, hogy a bolha

Q

-ra lépve legfeljebb az

n

-edik,

R

-re lépve pedig legfeljebb a

k

-adik lépésben elpusztul. Ekkor viszont a bolha

P

-re lépve legfeljebb a max

(n, k)

-adik lépésben (akár

Q

-ra, akár

R

-re lép tovább) mindenképpen elpusztul, vagyis

P

sem lehet " jó'' rácspont.

Ezután már nem nehéz a bolha túlélési stratégiáját megadni: ugorjon mindig "jó'' rácspontra.