Kezdőlap


Feladat:	F.2828	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Csekő Zoltán , Csörnyei Marianna , Imreh Csanád , Lente Gábor , Olaszi Zsolt , Reiff Ádám
Füzet:	1991/október, 306 - 308. oldal		PDF \| MathML
Témakör(ök):	Súlypont, Koordináta-geometria, Négyszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1990/december: F.2828

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $E F$ szakasz felezőpontja $I$ , $G E$ felezőpontja pedig $H$ . Mivel $I$ az $A C$ -nek is felezőpontja, az $E F G$ és $A C G$ háromszögek $S$ súlypontja közös.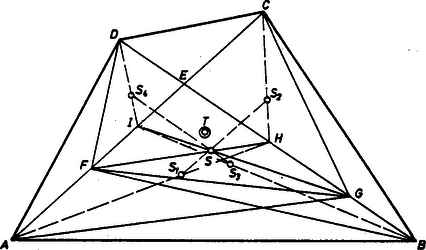

1. ábra

S

pont az

I G

szakasz 1:2 arányú osztópontja. Az

E F G

háromszög

H F

súlyvonala is átmegy

S

-en, ezért

S

H F

-et is 1:2 arányban osztja, s így súlypontja a

B D F

háromszögnek is. Ezzel az első állítást bebizonyítottuk.
A négyszög súlypontja rajta van a

B D A

háromszög

S_{1}

és a

B D C

háromszög

S_{2}

súlypontját összekötő egyenesen. Mivel

S_{1}

H A

szakasz,

S_{2}

pedig a

H C

szakasz

H

-hoz közelebbi harmadoló pontja,

S

pedig

H F

-en ugyanilyen arányú osztópont, ezért

S_{1} S_{2}

átmegy

S

-en. Ugyanígy mutatható meg, hogy az

A B C

és

A D C

háromszögek súlypontját összekötő egyenes is átmegy

S

-en. Ezért

S

a négyszögnek is súlypontja.

II. megoldás. Vegyünk fel egy ‐ általában ‐ ferdeszögű koordináta-rendszert a négyszög átlóira illeszkedő tengelyekkel (2. ábra).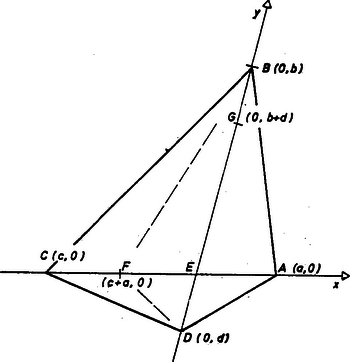

2. ábra

Legyen az első tengely

A C

A

és

C

abszcisszája

a

c

, továbbá

B

D

ordinátája

b

d

. Ebben a koordináta-rendszerben a súlypont koordinátáit ugyanúgy számítjuk ki, mint derékszögűben. Az

E

pont koordinátái: (0; 0), az

F

ponté:

(a + c; 0)

, végül a

G

ponté

(0; b + d)

. Ezért az

A C G

, a

B D F

és az

E F G

háromszögek súlypontjának koordinátái valóban egyezően:

\begin{matrix} (\frac{a + c}{3}; \frac{b + d}{3}) . \end{matrix}

A B D

B C D

A B C

és

A C D

háromszögek súlypontja rendre

\begin{matrix} S_{1} (\frac{a}{3}; \frac{b + d}{3}), S_{2} (\frac{c}{3}; \frac{b + d}{3}), S_{3} (\frac{a + c}{3}; \frac{b}{3}), S_{4} (\frac{a + c}{3}; \frac{d}{3}) . \end{matrix}

Látható, hogy

S_{1} S_{2}

párhuzamos az

x

S_{3} S_{4}

pedig az

y

tengellyel. Ezért

S_{1} S_{2}

és

S_{3} S_{4}

metszéspontja

(a + c) / 3; (b + d) / 3,

tehát ez a négyszöglemez súlypontja.

Olaszi Zsolt (Székesfehérvár, Teleki Blanka Gimn., III. o. t.)

Megjegyzés. Vázoljuk a látottak mechanikai jelentését. Az

A B C

homogén háromszöglemez

S

súlypontja ugyanott van, mint az

A

B

és

C

-be helyezett egységnyi tömegpontokból álló rendszerre ható súlyok (párhuzamos erők) eredőjének támadópontja. (Tetszőleges

O

kezdőpontot véve az

(\vec{O A} + \vec{O B} + \vec{O C}) : 3 = \vec{O S}

vektor az utóbbit határozza meg.) Ha ugyanis az

A B

oldal felezőpontja

F

, és a lemezt

A B

-vel "párhuzamosan'' keskeny trapézokra, vékony pálcákra osztjuk, mindegyiknek a súlypontja a felezőpontjában lesz, az

F C

szakaszra esik, az

A B

oldalhoz tartozó súlyvonalra, stb. ‐ Három tömegpont esetében az

A

-ra és

B

-re ható erők eredője 2-szer akkora, mint bármelyikükre külön, támadópontja

F

. Az

A

B

C

rendszerre ható súlyok támadópontja pedig az

F C

szakaszt 1:2 arányban osztja.

Ezekkel szemben homogén, konvex négyszöglemez és a csúcsaiba helyezett egységnyi tömegek esetében általában nincs meg a fenti egyezés, csak bizonyos "szabályos'' esetekben. Az

\vec{A F} = \vec{E C}

egyezés a 2. ábra esetében azt jelenti, hogy

A C

-vel párhuzamos pálcákra bontással elvesszük a

B D A

háromszöget és a vele egyenlő területű (és nyomatékú) konkáv

B C D F

négyszöget.

S

megkapható a maradék

B D F

háromszögből. (A mechanikai értelmezés az olvasóra marad).

Négy tömegpont esetén az

A

B

C

részrendszer súlypontja az 1. ábrán

S_{3}

, itt 3-szor akkora eredő hat, mint

D

-ben, a teljes pontrendszer súlypontja az

S_{3} D

szakasz 1:3 arányú negyedelő pontja. Ide esik az

S_{1} C

S_{2} A

és

S_{4} B

szakaszok negyedelő pontja is. (Az 1. ábrán

T

.) Mit jelent ez koordinátákban?

Lényegesen más a probléma, ha az idom kerületét tekintjük mint homogén rudak együttesét. Ennek súlypontja általában már háromszög esetében sem esik egybe a lemez súlypontjával.
B.T.