Feladat: F.2827 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Cserháti Vencel ,  Magó Kálmán ,  Ratkó Éva 
Füzet: 1991/október, 305 - 306. oldal  PDF  |  MathML 
Témakör(ök): Trigonometriai azonosságok, Trapézok, Húrnégyszögek, Vektorok skaláris szorzata, Feladat
Hivatkozás(ok):Feladatok: 1990/december: F.2827

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A feladat feltétele azt jelenti, hogy

cosα+cosβ+cosγ+cosδ=0,(1)
ahol α, β, γ, δ a négyszög egymás utáni csúcsainál lévő szögek. Alkalmazzuk a cosα+cosβ szorzattá alakítására vonatkozó azonosságot. Ekkor (1) így alakul:
2⋅cosα+β2⋅cosα-β2+2⋅cosγ+δ2⋅cosγ-δ2=0.

Mivel γ+δ=360∘-(α+β), azért
2⋅cosα+β2⋅cosα-β2-2⋅cosα+β2⋅cosγ-δ2=0,
amiből
cosα+β2(cosα-β2-cosγ-δ2)=0.
Ez pontosan akkor teljesül ha,
vagy  cosα+β2=0,vagy  cosα-β2=cosγ-δ2.

Az első esetben α+β=180∘ (mivel α, β konvex szögek, nincs egyéb lehetőség). Ekkor a négyszög trapéz. A második esetben |α-β2|=|γ-δ2| következik. Ez azt jelenti, hogy α-β=γ-δ, vagy α-β=δ-γ, azaz α+δ=β+γ vagy α+γ=β+δ. Itt az első eset ismét azt jelenti, hogy a négyszög trapéz, a második pedig azt, hogy húrnégyszög.
 
 Cserháti Vencel (Jászberény, Lehel Vezér Gimn., IV. o. t.) dolgozata alapján
 

II. megoldás. Használjuk az ábra jelöléseit. Az (1)-ben szereplő koszinuszértékeket az oldalakra illeszkedő vektorok skaláris szorzatával fejezhetjük ki, pl.
a→⋅b→=a⋅b⋅cos(180∘-α), ahol a és b a megfelelő vektorok hossza.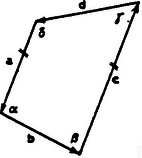
 
 

Ezért cosα=-a→⋅b→a⋅b. Ezután az (1) feltételt így írhatjuk:
a→⋅b→a⋅b+b→⋅c→b⋅c+c→⋅d→c⋅d+d→⋅a→d⋅a=0,
amiből
c⋅d⋅a→⋅b→+a⋅d⋅b→⋅c→+a⋅b⋅c→⋅d→+b⋅c⋅d→⋅a→=0.

Ennek bal oldalát szorzattá alakíthatjuk:
(d⋅b→+b⋅d→)(c⋅a→+a⋅c→)=0.

Ez utóbbi kétféleképpen állhat fenn:
 

Az első eset az, hogy a bal oldal valamelyik tényezője zérusvektor, azaz d⋅b→+b⋅d→=0→ vagy ac(a→a+c→c)=0,a→a=-c→c. Ez csak úgy lehetséges, ha b→∥d→vagya→∥c→, amikor is a négyszög trapéz.
 

A második esetben c⋅a→+a⋅c→ merőleges d⋅b→+b⋅d→-re és feltehetjük, hogy az ABCD négyszög nem trapéz, vagyis létezik a szemközti oldalpárok E és F metszéspontja.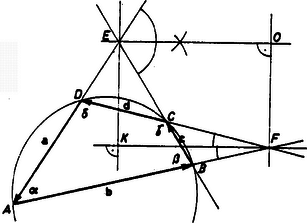
 
 

Az a⋅c→ és c⋅a→ vektorok hossza egyenlő, így ezek összege az E pontnál keletkező egyik szög EO szögfelezőjével párhuzamos. Hasonlóan d⋅b→ és b⋅d→ összege az FO szögfelezővel párhuzamos. Ezért EO⊥FO, de akkor EK⊥FK is fennáll, ahol EK és FK is szögfelezők. Könnyen láthatjuk, hogy AEK∢=(180∘-α-β)/2 és AFK∢=(180∘-α-δ)/2. Az AFKE négyszögben a belső szögek összege 360°, tehát
180∘-α-β2+180∘-α-δ2+α+270∘=360∘,
amiből β+δ=180∘, a négyszög húrnégyszög.
 
 Ratkó Éva (Bp., Berzsenyi D. Gimn., III. o. t.) dolgozata alapján