Feladat: F.2821 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Fleiner Balázs ,  Jakab Csaba ,  Pomozi István 
Füzet: 1991/október, 304. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai bizonyítások, Körök, Középponti és kerületi szögek, Háromszögek hasonlósága, Thalesz tétel és megfordítása, Háromszögek egybevágósága, Feladat
Hivatkozás(ok):Feladatok: 1990/november: F.2821

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen O a k kör középpontja, továbbá P, illetve Q az O-ból EC-re, illetve DG-re állított merőleges talppontja. Így P és Q felezi is az EC-t, illetve D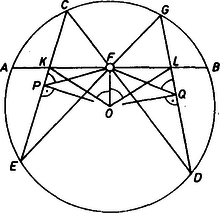G-t.

 
 

Használjuk az ábra további jelöléseit is. A CG és ED íveken nyugvó kerületi szögek egyenlősége révén EFC és DFG hasonló háromszögek. E két hasonló háromszögben FP és FQ egymásnak megfelelő súlyvonalak, ezért
FPC∢=FQG∢.(1)

Thalész tétele szerint OPKF és OFLQ húrnégyszög, azaz KOF∢=FPC∢ és FOL∢=FQG∢, így (1) alapján KOF∢=FOL∢, következésképpen az FOL és FOK háromszögek egybevágók, hiszen megegyeznek egy oldalban és a rajta fekvő két szögben. Tehát FK=FL, ami a feladat állítása. (Megoldásunk ugyanígy mondható el, ha P a KC, illetve Q az LG szakasz pontja.)