Kezdőlap


Feladat:	F.2817	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Erben Péter , Fleiner Balázs , Futó Gábor , Horváth István , Imreh Csanád , Kovács Flórián , Lente Gábor , Magó Kálmán , Miklós György , Papolczy Péter , Pór Attila
Füzet:	1991/szeptember, 257 - 258. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Számtani-mértani egyenlőtlenségek, Szélsőérték-feladatok differenciálszámítás nélkül, Diszkusszió, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1990/október: F.2817

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Szerkesszük meg a $C D$ egyenesen azt az $R$ és $P$ pontot, amelyre $A R P ∢ = B P R ∢ = α$ , ahol $α$ az a szög, amelyben $M$ -ből az $A B$ szakasz látszik.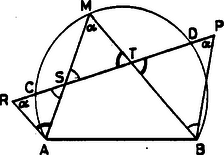

1. ábra

Az 1. ábrán egy és két ívvel jelölt csúcsszögek egyenlősége folytán az

R A S

és a

P T B

háromszögek hasonlóak. Ezért

R S : A R = P B : T P

, amiből

R S \cdot T P = A R \cdot P B

.
A számtani és mértani közép közötti egyenlőtlenség szerint:

\begin{matrix} \frac{R S + T P}{2} ≧ \sqrt[]{R S \cdot T P} = \sqrt[]{A R \cdot P B}, \end{matrix}

(1)

és itt

A R \cdot P B

állandó.

(1)

-ben egyenlőség pontosan akkor áll fenn, ha

R S = T P = \sqrt[]{A R \cdot P B}

. Ezután az

S T

szakaszt így becsülhetjük:

\begin{matrix} S T = R P - (R S + T P) ≦ R P - 2 \sqrt[]{A R \cdot P B}, \end{matrix}

tehát

S T

maximuma:

R P - 2 \sqrt[]{A R \cdot P B},

és ezt akkor kapjuk, ha

R S = T P = \sqrt[]{A R \cdot P B} .

\sqrt[]{A R \cdot P B}

szakasz megszerkeszthető. Ezt

P R

-re az

R

és

P

felől felmérve kapjuk az

S'

és

T'

pontokat, amelyekre

S' T'

maximális. Meg kell még mutatnunk, hogy ezekhez a pontokhoz létezik a köríven megfelelő

M

pont. Mindenekelőtt megmutatjuk, hogy

\sqrt[]{A R \cdot P B} ≦ R P / 2.

Legyen ugyanis

M

C D

ív egy tetszőleges pontja, és a hozzá tartozó metszéspontok

S

és

T

. Ekkor

\begin{matrix} \sqrt[]{A R \cdot P B} = \sqrt[]{R S \cdot T P} ≦ \sqrt[]{R S \cdot S P} ≦ \frac{R S + S P}{2} = \frac{R P}{2} . \end{matrix}

Ebből következik, hogy az

R P

szakaszon az előbb megszerkesztett

S'

és

T'

pontok sorrendje a következő:

R, S', T', P .

Tekintsük ezután az

A R S'

és

T' P B

háromszögeket. Ezek oldalaira:

\begin{matrix} \frac{A R}{R S'} = \frac{A R}{\sqrt[]{A R \cdot P B}} = \sqrt[]{\frac{A R}{P B}}, illetve \frac{T' P}{P B} = \frac{\sqrt[]{A R \cdot P B}}{P B} = \sqrt[]{\frac{A R}{P B}}, \end{matrix}

tehát két oldalpárjuk aránya megegyezik és a közbezárt

α

szög is egyenlő. Ezért e két háromszög hasonló, s így szögeik megegyeznek. Az

S'

-nél és

T'

-nél lévő csúcsszögeket figyelembe véve az

A S'

és

B T'

egyenesek metszik egymást egy

M'

pontban és a

T' M' S'

háromszög is hasonló az előző kettőhöz. De akkor az

M'

csúcsánál lévő szög

α

, tehát

M'

rajta van a köríven.

Papolczy Péter (Bp., Berzsenyi D. Gimn., IV. o. t.)

II. megoldás. Legyen először

C A = B D

, ekkor

C D ∣ ∣ A B

. Az

M

pont távolsága a

C D

egyenestől legyen

x

A B

és

C D

, távolsága pedig

d

.
Az

M S T

és

M A B

háromszögek hasonlósága miatt

\begin{matrix} \frac{S T}{A B} = \frac{x}{x + d} = \frac{1}{1 + \frac{d}{x}}, \end{matrix}

amelyből látjuk, hogy

S T

akkor maximális, ha

x

is az, és ebben az esetben

M

C D

ív felezőpontja.
Az általános esetre térve feltehetjük, hogy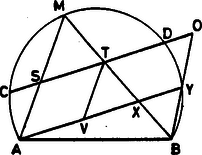

C A < B D

2. ábra

Húzzunk párhuzamost

A

-n keresztül

C D

-vel. Messe ez

M B

-t

X

-ben, a körívet pedig

Y

-ban (2. ábra). Az

A M

-mel

T

-n át húzott párhuzamos messe

A Y

-t a

V

pontban.
Nyilvánvaló, hogy

A V + V Y

állandó, továbbá az

A S T V

paralelogrammából

S T = A V

. Ezért

S T

akkor lesz maximális, ha

V Y

minimális. Könnyen látható, hogy

V T B ∢ = V Y B ∢

, hiszen a bal oldalon lévő szög egyállású az

A M B

szöggel, a jobb oldali pedig egy íven nyugvó kerületi szög ugyanezzel. Ezért a

B, Y, V, T

pontok egy körön vannak. Keresnünk kell egy olyan kört, amely átmegy a

B

és

Y

pontokon, van közös pontja

C D

-vel, és az

A Y

húrt egy

Y

-tól különböző

V

pontban metszi, úgy, hogy a

V Y

szakasz hossza minimális. Ha egy ilyen kör sugarát növeljük,

V Y

növekszik. Ezért

V Y

akkor lesz a legkisebb, ha a kör érinti a

C D

szakaszt.
Jelöljük a keresett érintési pontot

T_{1}

-gyel. Legyen a

B Y

és a

C D

egyenesek metszéspontja

O

. Az

O

pont biztosan létrejön, hiszen

B Y

és

C D

nem párhuzamosak. A körérintő és szelődarabok összefüggése alapján

O T_{1}^{2} = O Y \cdot O B

, ahonnan

O T_{1}

megszerkeszthető. Az

O T_{1}

szakaszt

O

-ból

C D

egyenesre mérve (

D

felé) kapjuk a

T_{1}

pontot, majd

C D

-re

T_{1}

-ben merőlegest állítva és ezt

B Y

felező merőlegesével elmetszve a keresett kör középpontját. A kör és

A Y

metszéspontja a

V_{1}

pont, az

A V_{1} = S_{1} T_{1}

összefüggés alapján pedig

S_{1}

is megszerkeszthető. Az elmondottakból következik, hogy az így szerkesztett

S_{1} T_{1}

valóban maximális. Meg kell még mutatnunk, hogy az

A S_{1}

és a

B T_{1}

egyenesek

M_{1}

metszéspontja az adott köríven van. Mivel

B, Y, T_{1}, V_{1}

egy körön helyezkednek el,

B Y V_{1} ∢ = V_{1} T_{1} B ∢

; továbbá

A S_{1}

párhuzamos

V T_{1}

-gyel, így

A M_{1} T_{1} ∢ = V_{1} T_{1} B ∢

. De akkor

A M_{1} T_{1} ∢ = B Y V_{1} ∢

, tehát

M_{1}

-ből

A B

ugyanakkora szögben látszik, mint az

Y

pontból, ezért

M_{1}

rajta van a köríven.

Kovács Flórián (Bp. Árpád Gimn., IV. o. t.) dolgozata alapján