Kezdőlap


Feladat:	F.2816	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kovács Flórián
Füzet:	1991/szeptember, 255 - 257. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Húrnégyszögek, Síkgeometriai számítások trigonometriával, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1990/október: F.2816

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ptolemaiosz tétele szerint bármely konvex húrnégyszög átlóinak szorzata egyenlő a szemközti oldalpárok szorzatainak összegével. Alkalmazzuk a tételt a $P A B C, P B C E$ és $P B C D$ húrnégyszögekre.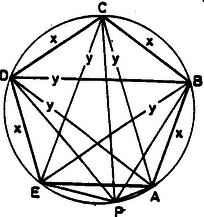

Az ábra jelöléseit is használva:

\begin{matrix} P A \cdot x + P C \cdot x & = P B \cdot y, \\ P E \cdot x + P B \cdot y & = P C \cdot y, \\ P B \cdot x + P D \cdot x & = P C \cdot y . \end{matrix}

A három egyenletet összeadva, majd mindkét oldalból

(P B + P C) \cdot y

-t levonva:

\begin{matrix} P A \cdot x + P C \cdot x + P E \cdot x = P B \cdot x + P D \cdot x, \end{matrix}

és ezt

x

-szel osztva a feladat állítását kapjuk.

II. megoldás. A feladat állításánál valamivel általánosabban azt fogjuk megmutatni, hogy a

2 n + 1

-oldalú

P_{0} P_{1} \dots P_{2 n}

szabályos sokszög

{\hat{P_{0} P}}_{2 n}

ívén lévő

P

pontra

\begin{matrix} P P_{0} + P P_{2} + \dots + P P_{2 n} = P P_{1} + P P_{3} + \dots + P P_{2 n - 1} . \end{matrix}

(1)

n = 2

esetben a feladat állítása.
Ismeretes, hogy az

r

sugarú körben a

2 α

középponti szöghöz tartozó húr hossza

2 r \cdot sin α .

Legyen a szabályos sokszög középpontja

O

és

P O P_{0} ∢ = 2 φ

. Ekkor az (1)-ben szereplő szakaszokat az említett módon felírva, majd

2 r

-rel osztva a következőt kapjuk:

\begin{matrix} sin φ + sin (\frac{2 \cdot 180^{\circ}}{2 n + 1} + φ) + \dots + sin (\frac{2 n \cdot 180^{\circ}}{2 n + 1} + φ) = \\ = sin (\frac{180^{\circ}}{2 n + 1} + φ) + sin (\frac{3 \cdot 180^{\circ}}{2 n + 1} + φ) + \dots + sin (\frac{(2 n - 1) \cdot 180^{\circ}}{2 n + 1} + φ) . \end{matrix}

Vonjuk ki mindkét oldalból a jobb oldalt, és csoportosítsunk úgy, hogy a

sin φ

tagon kívül a következő párok különbsége szerepeljen:
a bal oldal második tagjának és a jobb oldal utolsó tagjának különbsége, a bal oldal harmadik és a jobb oldal utolsó előtti tagjának különbsége s í.t. Ekkor a bal oldalon a

sin φ

tagon kívül

\begin{matrix} sin (\frac{2 i \cdot 180^{\circ}}{2 n + 1} + φ) - sin (\frac{2 (n - i) + 1}{2 n + 1} \cdot 180^{\circ} + φ) = \\ = sin (\frac{2 i \cdot 180^{\circ}}{2 n + 1} + φ) - sin (180^{\circ} - \frac{2 i \cdot 180^{\circ}}{2 n + 1} - φ) = \\ = sin (\frac{2 i \cdot 180^{\circ}}{2 n + 1} + φ) - sin (\frac{2 i \cdot 180^{\circ}}{2 n + 1} - φ) \end{matrix}

alakú kifejezések lesznek. Ezeket a

sin (α + φ) - sin (α - φ) = 2 \cdot cos α sin φ

azonosság segítségével átalakítva azt kell megmutatnunk, hogy

\begin{matrix} sin φ + (2 \cdot cos \frac{2 \cdot 180^{\circ}}{2 n + 1} + 2 \cdot cos \frac{4 \cdot 180^{\circ}}{2 n + 1} + \dots + 2 \cdot cos \frac{2 n \cdot 180^{\circ}}{2 n + 1}) \cdot sin φ = 0. \end{matrix}

(2)

P \equiv P_{0}

, azaz

sin φ = 0

, akkor (2) teljesül. Ha

sin φ \neq 0

, akkor

sin φ

-vel osztva, majd a

\begin{matrix} 2 \cdot cos \frac{2 i \cdot 180^{\circ}}{2 n + 1} = cos \frac{2 i \cdot 180^{\circ}}{2 n + 1} + cos (2 \cdot 180^{\circ} - \frac{2 i \cdot 180^{\circ}}{2 n + 1}) = \\ = cos \frac{2 i \cdot 180^{\circ}}{2 n + 1} + cos \frac{2 (2 n - i + 1) 180^{\circ}}{2 n + 1} \end{matrix}

átalakítást alkalmazva az

\begin{matrix} 1 + cos \frac{2 \cdot 180^{\circ}}{2 n + 1} + cos \frac{4 n \cdot 180^{\circ}}{2 n + 1} + cos \frac{4 \cdot 180^{\circ}}{2 n + 1} + cos \frac{(4 n - 2) \cdot 180^{\circ}}{2 n + 1} + \cdot \cdot \\ \dots + cos \frac{2 n \cdot 180^{\circ}}{2 n + 1} + cos \frac{(2 n + 2) \cdot 180^{\circ}}{2 n + 1} = 0 \end{matrix}

egyenlőséghez jutunk. Ezt rendezve, és

cos 0^{\circ} = 1

-et írva végül azt kell bizonyítanunk, hogy

\begin{matrix} cos 0^{\circ} + cos \frac{360^{\circ}}{2 n + 1} + cos 2 \cdot \frac{360^{\circ}}{2 n + 1} + cos 3 \cdot \frac{360^{\circ}}{2 n + 1} + \dots + cos 2 n \cdot \frac{360^{\circ}}{2 n + 1} = 0. \end{matrix}

(3)

Tekintsük ehhez azt a

2 n + 1

-oldalú szabályos sokszöget, amelynek középpontja az origó, egyik csúcsa pedig az

(1; 0)

pont. Tudjuk, hogy a szabályos sokszög középpontjából a csúcsokba mutató vektorok összege a zérusvektor. A

(3)

-ban szereplő összeg ennek a nullvektornak az

x

koordinátája, tehát zérus. Mivel pedig

(3)

ekvivalens

(1)

-gyel, így azt is igazoltuk.

Kovács Flórián (Bp., Árpád Gimn., IV. o. t.) dolgozata alapján

Megjegyzés. A

(2)

bal oldalán a zárójelben lévő összeg kiszámítható az

\begin{matrix} \frac{1}{2} + cos x + cos 2 x + \dots + cos n x = \frac{sin \frac{2 n + 1}{2} x}{2 \cdot sin \frac{x}{2}} \end{matrix}

azonosság alapján is. (Igazolása megtalálható Bogdán Z.: Matematika feladatok ‐ ötletek ‐ megoldások II. c. könyvben.)