Kezdőlap


Feladat:	F.2809	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Futó Tibor , Komócsi Sándor , Lente Gábor , Németh Sándor , Révész Ádám , Szalkai Ákos , Wiener Gábor
Füzet:	1991/október, 302 - 303. oldal		PDF \| MathML
Témakör(ök):	Szélsőérték-feladatok differenciálszámítás nélkül, Pitagorasz-tétel alkalmazásai, Háromszög-egyenlőtlenség alkalmazásai, Koordináta-geometria, Két pont távolsága, szakasz hosszúsága, Feladat
Hivatkozás(ok):	Feladatok: 1990/szeptember: F.2809

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.
Az 1. ábrán látható (esetleg elfajuló) háromszögre

\begin{matrix} O P + P A ≧ O A . \end{matrix}

(1)

1. ábra

Az itt szereplő távolságokat kifejezve (1) így alakul:

\begin{matrix} \sqrt[]{x^{2} + y^{2}} + \sqrt[]{{(a - x)}^{2} + {(b - y)}^{2}} ≧ \sqrt[]{a^{2} + b^{2}} . \end{matrix}

(2)

Mivel

x

és

y

nemnegatív számok, ezért

\begin{matrix} x + y = \sqrt[]{x^{2} + 2 x y + y^{2}} ≧ \sqrt[]{x^{2} + y^{2}}, \end{matrix}

(3)

így (2) és (3) alapján

\begin{matrix} z = x + y + \sqrt[]{{(a - x)}^{2} + {(b - y)}^{2}} ≧ \sqrt[]{x^{2} + y^{2}} + \sqrt[]{{(a - x)}^{2} + {(b - x)}^{2}} ≧ \sqrt[]{a^{2} + b^{2}} . \end{matrix}

Tehát

z

minimuma

\sqrt[]{a^{2} + b^{2}}

, amit nemnegatív

x

és

y

esetén az

x = y = 0

helyen vesz fel.

Németh Sándor (Győr, Révai M. Gimn. IV. o. t.)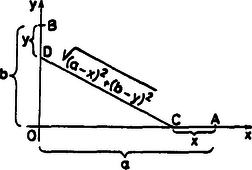

II. megoldás.

2. ábra

A 2. ábra jelöléseivel

\begin{matrix} z = A C + C D + D B = \\ = x + y + \sqrt[]{{(a - x)}^{2} + {(b - y)}^{2}}, \end{matrix}

z

tehát az

A C D B

töröttvonal hosszúsága. Ez nyilván akkor a legkisebb, ha a vonal egyenes szakasz, vagyis

\begin{matrix} z = A B = \sqrt[]{a^{2} + b^{2}} . \end{matrix}

Ez nemnegatív

x

és

y

esetében pontosan akkor következik be, ha

x = 0

és

y = 0

Megjegyzés: Mindkét megoldásban erősen kihasználtuk, hogy

x

és

y

nem negatív, hiszen pl. a II.-ban

x

is,

y

is szakasz hosszaként szerepelt. A feladat bizonyítása általánosítható a síkról a térre, vagy akár az

n

-dimenziós térre, így érvényes a következő:
Ha

a_{1}

a_{2}

\dots

a_{n}

adott valós számok,

x_{1}

x_{2}

\dots

x_{n}

pedig tetszőleges nemnegatív számok, akkor a

\begin{matrix} z = x_{1} + x_{2} + \dots + x_{n} + \sqrt[]{{(a_{1} - x_{1})}^{2} + {(a_{2} - x_{2})}^{2} + \dots + {(a_{n} - x_{n})}^{2}} \end{matrix}

kifejezés minimuma

\sqrt[]{a_{1}^{2} + a_{2}^{2} + \dots + a_{n}^{2}} .