Kezdőlap


Feladat:	F.2805	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Aranyi Ferenc , Aranyi Katalin , Balogh József , Bánfalvi Koppány , Borsányi Ákos , Erben Péter , Fügedi Zsolt , Hajnal József , Horváth István , Horváth Katalin , Kiss István , Kovács Ágnes , Kovács Péter , Kovács Vera , Kökényesi László , Lente Gábor , Magó Kálmán , Miklós György , Nagy Benedek , Papolczy Péter , Podoski Károly , Pór Attila , Pula Balázs , Turányi Zoltán , Ujváry-Menyhárt Zoltán , Virág Bálint , Wiener Gábor
Füzet:	1991/január, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Síkgeometriai szerkesztések, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1990/május: F.2805

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ismeretes, hogy a parabola fókuszából egy érintőjére állított merőleges talppontja a csúcsérintőn van. Ábránkon $F$ a parabola fókusza, $d$ a vezéregyenes, $e$ a csúcsérintő, $e_{1}$ $e_{2}$ , $e_{3}$ pedig három érintő, amelyek $P_{1}$ , $P_{2}$ , $P_{3}$ pontokban metszik egymást. A fókuszból az érintőkre bocsátott merőlegesek talppontja $T_{1}$ , $T_{2}$ , $T_{3}$ , amelyek az említett tétel szerint a csúcsérintőkre illeszkednek. Bebizonyítjuk, hogy a parabola három érintője által meghatározott háromszög körülírt köre átmegy az $F$ ponto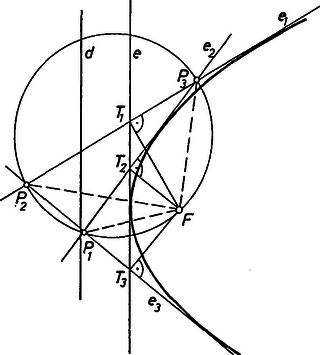n.

Thalesz tétele szerint

T_{1}

és

T_{2}

rajta van az

F P_{3}

átmérőjű körön, ezért az

F T_{1} T_{2}

és

F P_{3} T_{2}

szögek egyenlők. Hasonlóan

F P_{2}

Thalesz-köre tartalmazza a

T_{1}

és

T_{3}

pontokat, ezért

F T_{1} T_{3} ∢ = F P_{2} T_{3} ∢

. Így

F T_{1} T_{2} ∢ = F T_{1} T_{3} ∢

, ezért

F P_{3} T_{2} ∢ = F P_{2} T_{3} ∢

. A két utóbbi szög az a két szög, amelyben

P_{3}

-ból, illetve

P_{2}

-ből az

F P_{1}

szakasz látszik. Ezért az

F

P_{1}

P_{2}

P_{3}

pontok egy körön helyezkednek el. Ábránk betűzése ugyanis olyan, hogy

T_{3}

fölött van

T_{2}

, afölött pedig

T_{1}

, így

P_{2}

és

P_{3}

F P_{1}

egyenesnek ugyanabban a félsíkjában van.
Vegyünk ezután a négy érintőből hármat-hármat. Mivel az érintők között párhuzamosak nem lehetnek, három érintő egy háromszöget határoz meg. A két érintőhármas által meghatározott két háromszög köré írt köre az előbbiek szerint átmegy a parabola fókuszán, ezért egyik közös pontjuk a fókusz. A másik közös pont nyilván valamelyik két érintő metszéspontja, ezért a négy érintő által meghatározott négy lehetséges háromszög köré írt köröknek (sőt már háromnak is) egyetlen közös pontja lesz, a parabola fókusza. Ebből a közös pontból állítsunk merőlegest két érintőre. Ezeknek a merőlegeseknek a talppontja meghatározza a csúcsérintőt. Húzzunk merőlegest az ötödik érintő megadott irányára. Ennek a merőlegesnek és a csúcsérintőnek a közös pontja az ötödik érintőnek is pontja. Ezen a ponton át az ötödik érintő irányával párhuzamost húzva kapjuk az ötödik érintőt.
Ha a megadott négy érintő és az ötödik iránya páronként nem párhuzamos egyenesek, és a négy érintő közül semelyik három nem megy át egy ponton, akkor a feladatnak egy megoldása van. Az

F

pontot ugyanis a lehetséges négy kör egyértelműen meghatározza, és ezután egyértelmű a csúcsérintő, majd az ötödik érintő szerkesztése is. Egyéb esetekben pedig nincs megoldás.

Miklós György (Bp., I. István Gimn., III. o. t.)