Kezdőlap


Feladat:	F.2798	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Földesi Gábor , Hajnal Ákos , Kiss István , Kovács Ágnes , Podoski Károly , Pór Attila , Ujváry-Menyhárt Zoltán , Virág Bálint
Füzet:	1991/április, 155 - 156. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Egyenesek egyenlete, Hiperbola egyenlete, Feladat
Hivatkozás(ok):	Feladatok: 1990/április: F.2798

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $x \cdot y = 1$ egyenletű hiperbola úgynevezett "egyenlő szárú'' hiperbola, amelynek tengelyei egyenlők. Valós tengelye az $(1; 1)$ és $(- 1; - 1)$ pontok közötti szakasz, amelynek hossza: $2 a = 2 \sqrt[]{2} .$ Ezért a képzetes tengely: $2 b = 2 \sqrt[]{2} .$ Ismeretes, hogy minden hiperbolára $a^{2} + b^{2} = c^{2},$ ahol $c$ a fókuszok távolságának fele, így $c = 2.$ Ezért a két fókusz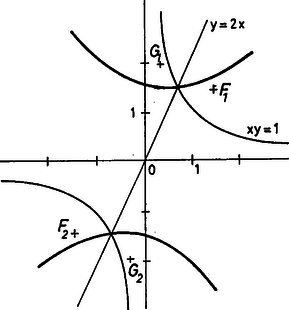: $F_{1} (\sqrt[]{2}; \sqrt[]{2}),$ illetve $F_{2} (- \sqrt[]{2}; - \sqrt[]{2})$ .

A tükörkép hiperbola tengelyeinek hossza nyilván változatlan, fókuszai legyenek

G_{1}

és

G_{2}

F_{1}

-et és

F_{2}

t az

y = 2 x

egyenesre tükrözve a

G_{1}

és

G_{2}

pontok koordinátái egyszerű számolással:

\begin{matrix} G_{1} (\frac{\sqrt[]{2}}{5}; \frac{7 \sqrt[]{2}}{5}) illetve G_{2} (- \frac{\sqrt[]{2}}{5}; - \frac{7 \sqrt[]{2}}{5}) . \end{matrix}

A hiperbola definíciója szerint a

G_{1}, G_{2}

fókuszú és

2 a = 2 \sqrt[]{2}

valós tengelyű hiperbola éppen azokat a P(x; y) pontokat tartalmazza, amelyekre:

\begin{matrix} G_{1} P - G_{2} P = 2 \sqrt[]{2} vagy G_{2} P - G_{1} P = 2 \sqrt[]{2} . \end{matrix}

(1)

A hiperbola egyenlete ezért:

\begin{matrix} | \sqrt[]{{(x - \frac{\sqrt[]{2}}{5})}^{2} + {(y - \frac{7 \sqrt[]{2}}{5})}^{2}} - \sqrt[]{{(x + \frac{\sqrt[]{2}}{5})}^{2} + {(y + \frac{7 \sqrt[]{2}}{5})}^{2}} | = 2 \sqrt[]{2} . \end{matrix}

(2)

Négyzetre emelve és rendezve:

\begin{matrix} x^{2} + y^{2} = \sqrt[]{{(x - \frac{\sqrt[]{2}}{5})}^{2} + {(y - \frac{7 \sqrt[]{2}}{5})}^{2}} \cdot \sqrt[]{{(x + \frac{\sqrt[]{2}}{5})}^{2} + {(y + \frac{7 \sqrt[]{2}}{5})}^{2}} . \end{matrix}

(3)

A (3) egyenlet az (1)-ben (illetve (2)-ben) "vagy''-gyal kapcsolt két egyenlet következménye, de (3)-ból is következik az (1)-ben szereplő két egyenlet. Ezért (1), (2) és (3) páronként ekvivalensek. Mivel (3) mindkét oldala nemnegatív, négyzetre emelése után vele ekvivalens egyenlethez jutunk:

\begin{matrix} {(x^{2} + y^{2})}^{2} = (x^{2} + y^{2} + 4 - \frac{2 x \sqrt[]{2}}{5} - \frac{14 y \sqrt[]{2}}{5}) \cdot (x^{2} + y^{2} + 4 + \frac{2 x \sqrt[]{2}}{5} + \frac{14 y \sqrt[]{2}}{5}) . \end{matrix}

Ebből

\begin{matrix} {(x^{2} + y^{2})}^{2} = {(x^{2} + y^{2} + 4)}^{2} - {(\frac{2 x \sqrt[]{2}}{5} + \frac{14 y \sqrt[]{2}}{5})}^{2}, \end{matrix}

amiből

\begin{matrix} 8 x^{2} + 8 y^{2} + 16 = \frac{8 x^{2} + 2 \cdot 56 x y + 8 \cdot 49 y^{2}}{25} . \end{matrix}

Végül rendezés után a tükörkép hiperbola egyenlete:

\begin{matrix} 12 y^{2} + 7 x y - 12 x^{2} = 25. \end{matrix}

Pór Attila (Bp., Fazekas M. Gyak. Gimn., II. o. t.)

II. megoldás. Legyen az

x \cdot y = 1

egyenletű hiperbola tetszőleges pontja

P_{0} (x_{0}; y_{0}),

ennek tükörképe az

y = 2 x

egyenletű egyenesre

P (x; y) .

Mivel a

P_{0} P

egyenes merőleges az

y = 2 x

-re, iránytangense

- 1 / 2

, és így

\begin{matrix} \frac{y - y_{0}}{x - x_{0}} = - \frac{1}{2} . \end{matrix}

(4)

P_{0} P

szakasz

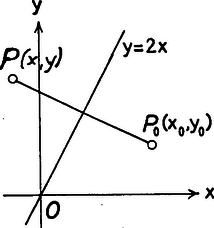(\frac{x_{0} + x}{2}; \frac{y_{0} + y}{2})

felezőpontja rajta van az

y = 2 x

egyenesen, ezért

\begin{matrix} \frac{y + y_{0}}{2} = 2 \cdot \frac{x + x_{0}}{2} . \end{matrix}

(5)

A (4) és (5)-ből álló egyenletrendszer megoldásaként az eredeti koordináták az újakkal kifejezve:

\begin{matrix} x_{0} = \frac{4 y - 3 x}{5}; \end{matrix}

Tekintve, hogy

x_{0} \cdot y_{0} = 1,

a tükörkép hiperbola egyenlete

\begin{matrix} \frac{4 y - 3 x}{5} \cdot \frac{4 x + 3 y}{5} = 1, \end{matrix}

amelyből

\begin{matrix} 12 y^{2} + 7 x y - 12 x^{2} = 25. \end{matrix}