Kezdőlap


Feladat:	F.2793	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Benczúr Péter , Bíró Norbert , Podoski Károly , Ujváry-Menyhárt Zoltán
Füzet:	1991/április, 151 - 153. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Trigonometriai azonosságok, Húrnégyszögek, Érintőnégyszögek, Szinusztétel alkalmazása, Szögfüggvények, síkgeometriai számítások, Síkgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1990/március: F.2793

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A feladat megoldása érdekében először azt mutatjuk meg, hogy minden érintőnégyszögben a szemközti érintési pontokat összekötő szakaszok metszéspontján mindkét átló átmegy. Használjuk az 1.ábra jelöléseit.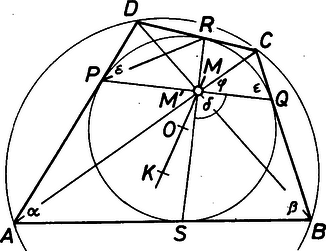

1. ábra

Jelölje

A C

és

P Q

metszéspontját

M

. A

P

illetve

Q

pontban érintő oldalak

P Q

-val egyenlő szöget zárnak be, így az

A M P

és

C M Q

háromszögekre a szinusztételt alkalmazva:

\begin{matrix} A M / A P = sin ϵ / sin φ = C M / C Q, amiből A M / C M = A P / C Q . \end{matrix}

(1)

Legyen

A C

és

R S

metszéspontja

M'

. Ekkor az előzőkhöz hasonlóan kapjuk, hogy

A M' / A S = C M' / C R .

Mivel a körhöz külső pontból húzott érintőszakaszok egyenlő hosszúak,

A S = A P

és

C R = C Q,

ezért

\begin{matrix} A M' / C M' = A P / C Q . \end{matrix}

(2)

(1) és (2) összehasonlításából

M = M',

tehát az

A C

átló átmegy

P Q

és

R S

metszéspontján. Ugyanezt elmondhatjuk

B D

-ről is, tehát

R S

és

P Q

valóban áthaladnak az

M

ponton.
Ezután bebizonyítjuk, hogy ha egy érintőnégyszög húrnégyszög, akkor a szemközti érintési pontokat összekötő szakaszok merőlegesek egymásra.
Mivel

α + γ = 180^{\circ}

, a beírt kör

\hat{S P}

és

\hat{R Q}

ívéhez összesen ugyancsak 180

°

középponti szög tartozik. A megfelelő kerületi szögek összege így ennek fele: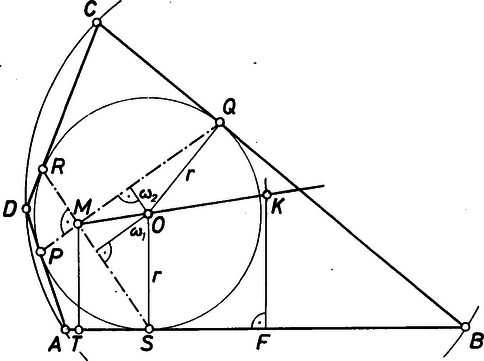

\begin{matrix} P R S ∢ + R P Q ∢ = 90^{\circ} . \end{matrix}

Mivel

P R S ∢ = P R M ∢

és

R P Q ∢ = R P M ∢,

ezért

P Q

és

R S

valóban merőlegesek.

2. ábra

Végül igazoljuk, hogy a négyszög köré írt kör középpontja az

M O

egyenesen van. Az

A B

oldalfelező merőlegesének

M O

-val való metszéspontját jelölje

K,

M,

K

pontok merőleges vetülete az

A B

egyenesen

T

, ill. F (2. ábra). A párhuzamos szelők tétele szerint

\begin{matrix} M O / O K = T S / S F . \end{matrix}

(3)

Célunk a jobb oldalon álló arány meghatározása. Nyilván

S R = 2 r sin ω_{1},

így

\begin{matrix} S M = R sin ω_{1} + r cos ω_{2}, \end{matrix}

(4)

ezért (a merőleges szárú

A S M

és

ω_{1}

szögekkel)

\begin{matrix} T S = S M \cdot cos ω_{1}, \end{matrix}

azaz (4) szerint

\begin{matrix} T S = r cos ω_{1} (sin ω_{1} + cos ω_{2}) . \end{matrix}

(5)

A P O S

deltoidban

A O

szögfelező, ahonnan

\begin{matrix} A S = r \end{matrix}

(6)

hasonlóan

\begin{matrix} S B = r \end{matrix}

(7)

(6) és (7) alapján

\begin{matrix} S F = \frac{1}{2} (S B - S A) = - \frac{r}{2} (tg \frac{ω_{1} + ω_{2} + 90^{\circ}}{2} + tg \frac{ω_{1} - ω_{2} + 90^{\circ}}{2}) . \end{matrix}

Felhasználva a

tg α + tg β = sin (α + β) / cos α cos β

és a

2 cos α cos β = cos (α + β) + cos (α - β)

azonosságokat,

\begin{matrix} S F = - r \frac{sin (ω_{1} - 90^{\circ})}{cos (ω_{1} + 90^{\circ}) + cos ω_{2}} = r \frac{cos ω_{1}}{sin ω_{1} - cos ω_{2}} \end{matrix}

adódik, ebből pedig (3) és (5) felhasználásával

\begin{matrix} \frac{M O}{O K} = \frac{T S}{S F} = sin^{2} ω_{1} - cos^{2} ω_{2} . \end{matrix}

Ha ezek után

K'

B C

oldal felező merőlegesének

O M

-mel való metszéspontját jelöli, akkor

M O / O K'

értéke

ω_{1}

és

ω_{2}

szerepének felcserélésével kapható:

\begin{matrix} \frac{M O}{O K'} = sin^{2} ω_{2} - cos^{2} ω_{1} = (1 - cos^{2} ω_{2}) - (1 - sin^{2} ω_{1}) = sin^{2} ω_{1} - cos^{2} ω_{2} = \frac{M O}{O K}, \end{matrix}

tehát

K = K'

. A négyszög köré írt kör középpontja így valóban az

M O

egyenesen van.

Benczúr Péter (Bp., Fazekas M. Gyak. Gimn., IV. o. t.) dolgozata alapján

Megjegyzés. A vizsgált típusú négyszögekkel kapcsolatban megemlítünk egy érdekes tételt, az 1960. évi szeptemberi számunk 24. oldalán megoldott 599. gyakorlatot:
Az

A B C D

húrnégyszög

A C

és

B D

átlói merőlegesek,

F

metszéspontjuknak az oldalakon való vetületei

P, Q, R, S .

Bizonyítsuk be, hogy a

P Q R S

négyszög húrnégyszög és egyben érintőnégyszög (idegen szóval bicentrikus, két középponttal bíró négyszög).
Következő számunkban több más idevágó régi feladatunkat is felidézzük.