Kezdőlap


Feladat:	F.2779	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Aranyi F. , Bánfalvi K. , Benczúr P. , Egri Ilona , Erben P. , Faragó Éva , Fügedi Zs. , Hajnal Á. , Harcos G. , Horváth I. , Kiss 128 István , Kónya I. , Kovács 113 Vera , Kovács 271 Ágnes , Lénárt L. , Magó K. , Molnár L. , Papolczy P. , Pócs M. , Podoski Károly , Pór A. , Prikler Gy. , Ruda G. , Sági Z. , Szász Éva , Székely-Doby András , Szekeres B. , Tokodi T. , Turányi Z. , Újváry-Menyhárt Zoltán , Varga Mónika , Virág A. , Weisz Cs.
Füzet:	1990/november, 376 - 377. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Trapézok, Négyszögek középvonalai, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1990/január: F.2779

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen először $O B = 0$ . Ekkor az $O$ pont nem megoldás, mert a $B O A ∢$ határozatlan. Az egyetlen megoldás most az a $C$ pont lesz, amelyre $C A B ∢ = 30^{\circ}$ és $A C B ∢ = 60^{\circ}$ . Ez a $C$ pont könnyen megszerkeszthető.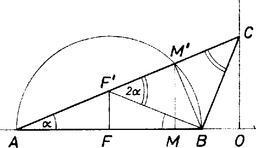
Ha $O B > 0$ , akkor az $O$ pont nyilván megoldás lesz, mert $B O A ∢ = 2 B A O ∢ = 0^{\circ}$ , és így az $O$ pontra teljesül a megkövetelt feltétel.

1. ábra

Keressünk ezután olyan

C

pontot, amely a derékszög másik szárán van, és

O

-tól különböző. Szerkesszük meg

A B

Thalész-körét, melynek középpontja legyen

F

. Az

O F

felezőmerőlegese messe a Thalész-kört az

M'

pontban. Állítjuk, hogy

A M'

a derékszög másik szárát a szerkesztendő

C

pontban metszi. Az 1. ábra jelöléseit használva láthatjuk, hogy

O F F' C

derékszögű trapéz, amelynek középvonala

M M'

. Ezért

C M' = M' F'

. A Thalész-kör folytán pedig

B M'

merőleges

C F'

-re, tehát a

B C F'

háromszög egyenlő szárú. Ugyancsak egyenlő szárú az

A B F'

áromszög, amelynek

A

-nál levő szögét

α

-val jelölve

B C F' ∢ = B F' C ∢ = 2 α

. Így

C

valóban a kívánt tulajdonságú pont.
Ez a

C

pont csak akkor létezik, ha

O M > O B

, azaz

\begin{matrix} \frac{O B + B F}{2} > O B, vagyis A B > 2 O B . \end{matrix}

Megfordítva, ha

A B > 2 O B

, akkor

O M > O B

, ahol

M

O F

felezőpontja. Így létezik

O F

felezőmerőlegesének és

A B

Thalész-körének (félkör)

M'

metszéspontja, és

A M'

, valamint a derékszög másik szárának

C

metszéspontja is, a fenti meggondolásunk szerint ekkor

B C A ∢ = 2 B A C ∢

teljesül.

Székely-Doby András (Bp., Petőfi S. Gimn., IV. o. t.)

dolgozata alapján

2. ábra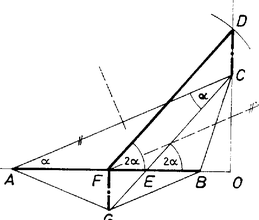

II. megoldás. Használjuk a 2. ábra jelöléseit. A speciális eseteket az I. megoldáshoz hasonlóan vizsgálhatjuk. Tegyük fel, hogy a derékszög másik szárán létezik a kívánt tulajdonságú,

O

-tól különböző

C

pont. Ekkor az

A B C

háromszög

C

-nél levő belső szögének felezője felezi a háromszög köré írt kör

C

-t nem tartalmazó

A B

ívét. Feltételeink szerint az ábrán

α

-val jelölt szögek egyenlők, és ezért a kerületi szögek tétele szerint

A G = G B = B C

, továbbá

G A B ∢ = G B A ∢ = B G C ∢ = α

, ami azt jelenti, hogy

A G B C

szimmetrikus trapéz. De akkor átlói egyenlők, azaz

A B = G C

. Toljuk el a

G C

szakaszt

G F

távolsággal, így kapjuk az

F D

szakaszt. Mivel az

A E C

háromszög

E

-nél levő külső szöge

2 α

, ezért

F D

2 α

szöget zár be

A B

-vel. Ezután megállapíthatjuk, hogy ha

C

megszerkeszthető, akkor megszerkeszthető az

A B

-vel azonos hosszúságú

F D

segítségével a

D

pont is, és

F D > F O

, azaz

A B > \frac{A B}{2} + B O

, amiből

A B > 2 O B

a szerkeszthetőség szükséges feltétele. Megmutatjuk, hogy ez a feltétel elegendő is.

3. ábra

Tegyük fel ugyanis, hogy

A B > 2 O B

. Az

F

köré rajzolt

A B

sugarú kör messe a derékszög másik szárát

D

-ben. A

D F O ∢ = 2 α

felezőjével ‐ a 3. ábrán szaggatott vonallal szerepel ‐

A

-n át húzott párhuzamos a derékszög másik szárát egy

C

pontban metszi. Toljuk el

F D

-t

D C

-vel, így kapjuk

F

képeként a

G

pontot. Messe

G C

A B

egyenest az

E

pontban. Az eltolás miatt

C E O ∢ = 2 α

, és mivel ez a szög az

A E C

háromszög külső szöge,

E C A ∢ = α

. Ez azt jelenti, hogy

A B

és

C G

A C

felezőmerőlegesére szimmetrikus szakaszok, vagyis

A G B C

szimmetrikus trapéz, ami köré kör írható. A kerületi szögek tétele szerint

G C B ∢ = α

, tehát

B C A ∢ = 2 α

. Ezért

C

a szerkesztendő pont.

III. megoldás. A speciális esetek vizsgálatát mellőzzük. A szerkesztést számítás alapján fogjuk elvégezni. Legyen

O C = x

O A = a

és

O B = b

. A 2. ábra alapján

C B O ∢ = 3 α

, továbbá

\begin{matrix} tg 3 α = \frac{x}{b}, tg α = \frac{x}{a} . \end{matrix}

\begin{matrix} tg 3 α = \frac{3 \cdot tg α - {tg}^{3} α}{1 - 3 \cdot {tg}^{2} α} \end{matrix}

azonosság miatt így

\begin{matrix} \frac{x}{b} = \frac{3 \cdot \frac{x}{a} - \frac{x^{3}}{a^{3}}}{1 - 3 \cdot \frac{x^{2}}{a^{2}}}, \end{matrix}

innen pedig

x = 0

, vagy

\begin{matrix} x = a \sqrt[]{\frac{a - 3 b}{3 a - b}}, \end{matrix}

ami megszerkeszthető.
A megoldhatóság feltétele:

a > 3 b

, azaz

A B > 2 O B