Feladat: F.2774 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Aranyi Katalin ,  Balogh 171 J. ,  Batthányi P. ,  Benczúr P. ,  Botrágyi T. ,  Cserháti V. ,  Erben P. ,  Fürjes A. ,  Hajnal Veronika ,  Harcos G. ,  Horváth I. ,  Imreh Cs. ,  Keresztély T. ,  Kiss 128 I. ,  Kiss 943 Orsolya ,  Kónya I. ,  Kórász T. ,  Kovács 271 Ágnes ,  Kovács 998 P. ,  Kovács F. ,  Magó K. ,  Matolcsi M. ,  Monori A. ,  Nagy 737 Gabriella ,  Papolczy P. ,  Parádi Cs. ,  Pócs M. ,  Podoski Károly. ,  Pór A. ,  Sági Z. ,  Szekeres B. ,  Szendrői B. ,  Turányi Z. ,  Újváry-Menyhárt Zoltán ,  Varga Mónika ,  Vass Zsófia ,  Weisz Cs. ,  Wiener G. ,  Zircher P. 
Füzet: 1990/november, 370 - 372. oldal  PDF  |  MathML 
Témakör(ök): Egyéb sokszögek hasonlósága, Trapézok, Feladat
Hivatkozás(ok):Feladatok: 1989/december: F.2774

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először azt mutatjuk meg, hogy ha egy konvex négyszöget szét lehet vágni egy egyenessel két hasonló négyszögre, akkor az trapéz. Használjuk az 1. ábra jelöléseit. A két négyszög hasonlóságából következik, hogy csúcsaikat egy körüljárás szerint felsorolva, azok úgy feleltethetők meg egymásnak, hogy az egy máshoz rendelt csúcsoknál fekvő szögek megegyeznek.

 
 

1. ábra
 

Az összes lehetséges esetet úgy találhatjuk meg, hogy pl. az AEFD négyszög A csúcsához hozzárendeljük a másik négyszög egy csúcsát ‐ ez négyféle lehetőség ‐ az E, F, D pontokhoz pedig rendre az A-hoz rendelt pontot valamelyik körüljárás szerint követő pontokat rendeljük. Mivel két irányban járhatjuk körül a második négyszöget, összesen 2⋅4=8 eset lesz.
1. Az AEFD, EBCF hasonlóságban A képe E, E képe B, F képe C és D képe F. Ezért α=ε, 180∘-ε=β, tehát α+β=180∘; az eredeti négyszög trapéz.
2. AEFD, EFCB, hasonlóságban α=ε, 180∘-ε=φ, 180∘-φ=γ, δ=β. Ezekből α=γ és δ=β, tehát az eredeti négyszög most paralelogramma, és így trapéz is.
3. Ha AEFD∼BCFE, akkor a α=β, 180∘-ε=γ, 180∘-φ=φ, δ=ε. Ezért most δ+γ=180∘, tehát a négyszög trapéz.
4. AEFD∼BEFC, ekkor α=β, 180∘-ε=ε, 180∘-φ=φ, δ=γ. Ebből α+δ=β+γ, így α+δ=180∘, a négyszög trapéz.
5. AEFD∼CFEB, ekkor α=γ, 180∘-ε=φ, 180∘-φ=ε, δ=β. Az előbbi esethez hasonlóan α+δ=180∘.
6. AEFD∼CBEF, akkor α=γ, 180∘-ε=β, 180∘-φ=ε, δ=φ. A második és harmadik összefüggésből φ=β, ezért ismét α+δ=β+γ=180∘.
7. AEFD∼FEBC, így α=φ, 180∘-ε=ε, 180∘-φ=β, δ=γ. Az első és harmadik egyenlőségből α+β=180∘, ezért a négyszög trapéz.
8. AEFD∼FCBE, ekkor α=φ, 180∘-ε=γ, 180∘-φ=β, δ=ε. Az előző esethez hasonlóan most is α+β=180∘.
Mindegyik esetben azt láttuk tehát, hogy az eredeti négyszög szükségképpen trapéz.
Ezután nézzük az állítás ,,akkor'' részét. Bebizonyítjuk, hogy minden trapéz egy egyenessel két hasonló trapézra vágható. A 2. ábra alapján a hasonlóság szükséges feltétele:
au=uc,azazu2=a⋅c.(1)
Ilyen u hosszúságú párhuzamos szakasz az a és c hosszúságú alapok között nyilván létezik. Ha a≠c, akkor pontosan egy ilyen szakasz húzható, a=c esetén pedig bármely ,,középpárhuzamos'' megfelelő.
 
 

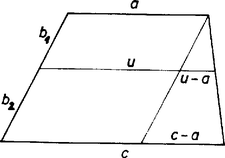2. ábra
 

A hasonlósághoz elegendő lesz, ha az egyértelműen adódó, ill. alkalmasan választott b1, b2 szakaszokra teljesül, hogy
b2b1=ua,(2)
hiszen a 2. ábra két részeként létrejött trapézokban a megfelelő szögek egyenlők.
Ha a=c=u, akkor nyilván b1=b2 megfelel. Tegyük fel, hogy a≠c, ekkor
c-au-a=b1+b2b1,
azaz
b2b1=c-au-a-1.(3)
Helyettesítsük be (1)-et (3)-ba, így
b2b1=c-aac-a-1=(c-a)(ac+a)ac-a2-1=ac+aa-1=aca=ua,
tehát az (1) feltétel ebben az esetben elegendő is a két trapéz hasonlóságához.