Kezdőlap


Feladat:	F.2763	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bíró N. , Kovács 998 P. , Podoski Károly. , Vass Zsófia
Füzet:	1990/április, 158 - 159. oldal		PDF \| MathML
Témakör(ök):	Középvonal, Szögfelező egyenes, Beírt kör, Párhuzamos szelők tétele, Feladat
Hivatkozás(ok):	Feladatok: 1989/október: F.2763

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit. Legyen a $B$ csúcsból induló szögfelező és a $H K$ középvonal metszéspontja $M$ . Messe a beírt kör $A B$ oldalon levő $P$ érintési pontját az $M$ ponttal összekötő egyenes az $A C$ oldalt a $Q$ pont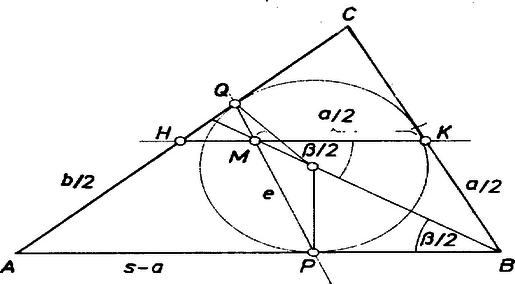ban.

Elegendő megmutatnunk, hogy

Q

a beírt körnek az

A C

oldalra illeszkedő érintési pontja. Mivel

P

érintési pont, ismert összefüggés szerint

A P = s - a

, ahol

s

a félkerület. Azt kell tehát igazolnunk, hogy

A Q = s - a

.
Könnyen látható, hogy az

M K B

háromszög egyenlő szárú, hiszen

M

-nél levő szöge és az egyik

β / 2

szög váltószögek. Ezért

M K = \frac{a}{2}

, így

\begin{matrix} H K = \frac{c}{2} alapján H M = \frac{c}{2} - \frac{a}{2} = \frac{c - a}{2} (ha c > a) . \end{matrix}

Mivel

A H = \frac{b}{2}

, a

Q H

szakaszra a párhuzamos szelők tétele szerint a következő összefüggést kapjuk:

\begin{matrix} \frac{Q H}{Q H + \frac{b}{2}} = \frac{H M}{A P}, azaz \frac{Q H}{Q H + \frac{b}{2}} = \frac{\frac{c - a}{2}}{s - a} . \end{matrix}

Ebből

\begin{matrix} Q H \cdot \frac{- a + b + c}{2} = (Q H + \frac{b}{2}) \cdot \frac{c - a}{2}, \\ Q H \cdot (\frac{- a + b + c}{2} - \frac{c - a}{2}) = \frac{b (c - a)}{4}, \\ Q H = \frac{c - a}{2} . \end{matrix}

Tehát

A Q = A M + H Q = \frac{b}{2} + \frac{c - a}{2} = s - a

, és ezt akartuk bizonyítani. (

c < a

esetén a bizonyítás lényegében ugyanaz).

Vass Zsófia (Szentendre, Ferences Gimn. IV. o. t.)