Kezdőlap


Feladat:	F.2757	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Becsei T. , Erben P. , Németh 026 L. , Podoski Károly , Tóth 509 P. Z.
Füzet:	1990/április, 156 - 157. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Háromszögek nevezetes tételei, Szögfelező egyenes, Prímtényezős felbontás, Feladat
Hivatkozás(ok):	Feladatok: 1989/szeptember: F.2757

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit. A $B D$ szögfelező a $b$ oldalt $x$ és $b - x$ részekre osztja. A szögfelezőre vonatkozó tétel szerint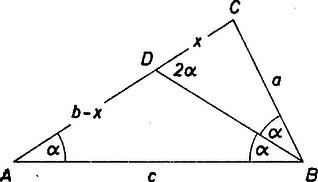

\begin{matrix} \frac{b - x}{x} = \frac{c}{a}, amiből \\ x = \frac{a \cdot b}{a + c} . & (1) \end{matrix}

A B C

és

B D C

háromszögek hasonlóságából

\frac{a}{b} = \frac{x}{a}

, innen (1) alapján

\frac{a}{b} = \frac{b}{a + c}

, azaz

\begin{matrix} a^{2} + a c = b^{2} . \end{matrix}

(2)

Jelölje

a

és

c

legnagyobb közös osztóját

k

, ekkor

\begin{matrix} a = k a_{1}, c = k c_{1}, \end{matrix}

(3)

és az

a_{1}

c_{1}

számok egymáshoz relatív prímek. (2) alapján ekkor

b^{2} = a^{2} + a c = k^{2} (a_{1}^{2} + a_{1} c_{1})

, tehát

\begin{matrix} a_{1}^{2} + a_{1} c_{1} = a_{1} (a_{1} + c_{1}) = b_{1}^{2} \end{matrix}

(4)

is négyzetszám, ahol nyilván

b = k b_{1}

. Mivel

a_{1}

-nek és

c_{1}

-nek nincs 1-nél nagyobb közös osztója, ezért

a_{1}

és

a_{1} + c_{1}

is relatív prímek; ezek szorzata,

b_{1}^{2}

csak úgy lehet négyzetszám, ha

a_{1}

és

a_{1} + c_{1}

is négyzetszám:

\begin{matrix} a_{1} = A^{2}, a_{1} + c_{1} = B^{2} . \end{matrix}

Ebből (3) és (4) alapján

a

b

c

-re azt kapjuk, hogy

\begin{matrix} a = k A^{2}, b = k A B, c = k (B^{2} - A^{2}) . \end{matrix}

(5)

a

b

c

értékek szükségképpen pozitívak, így

k > 0

;

A B > 0

miatt feltehető, hogy

A > 0

és

B > 0

, és ekkor

B > A

. A háromszög-egyenlőtlenség következtében

\begin{matrix} k (B + A) (B - A) = k (B^{2} - A^{2}) = c < a + b = k (A^{2} + A B) = k A (A + B), \end{matrix}

azaz

\begin{matrix} B - A < A, B < 2 A . \end{matrix}

Az eddigi tulajdonságok együttesen már elégségesek is ahhoz, hogy az

a

b

c

oldalakkal rendelkező háromszög eleget tegyen a feladat feltételeinek: ha ugyanis

k

A

és

B

olyan természetes számok, amelyekre fennáll

A < B < 2 A

, akkor a belőlük (5) szerint elkészített

a

b

c

(pozitív egész) számokra

a < b < a + c

és

c = k (B - A) \cdot (B + A) < k A (B + A) = a + b

;

a

b

c

tehát valóban egy háromszög oldalai, és (5)-ből láthatóan következik (2). Mivel

a < b

, ezért az

a

-val szemközti szög hegyesszög. A koszinusztétel értelmében

\begin{matrix} cos α = \frac{c^{2} + b^{2} - a^{2}}{2 b c} = \frac{c^{2} + a c}{2 b c} = \frac{a + c}{2 b} = \frac{b}{2 a}, \\ cos β = \frac{c^{2} + a^{2} - b^{2}}{2 a c} = \frac{c^{2} - a c}{2 a c} = \frac{c - a}{2 a}, \end{matrix}

így

\begin{matrix} cos 2 α = 2 cos^{2} α - 1 = \frac{b^{2}}{2 a^{2}} - 1 = \frac{b^{2} - 2 a^{2}}{2 a^{2}} = \frac{a c - a^{2}}{2 a^{2}} = \frac{c - a}{2 a} = cos β, \end{matrix}

tehát valóban

2 α = β

.
A feladat követelményeit ezek szerint azok a háromszögek elégítik ki, melyek oldalai

a = k A^{2}

b = k A B

és

c = k (B^{2} - A^{2})

, ahol

k

A

B

pozitív egészek és

A < B < 2 A