Kezdőlap


Feladat:	F.2756	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Boncz András , Botrágyi T. , Erdélyi Györgyi , Kovács T. , Podoski Károly. , Szalkai Á. , Tomacsek J. , Tóth 509 P. Z.
Füzet:	1990/március, 110. oldal		PDF \| MathML
Témakör(ök):	Menelaosz-tétel, Szögfelező egyenes, Párhuzamos szelők tételének megfordítása, Feladat
Hivatkozás(ok):	Feladatok: 1989/szeptember: F.2756

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a $C$ -nél levő szög felezője párhuzamos $A B$ -vel, akkor a belső szögfelező merőleges $A B$ -re, és ezért $A C = B C$ . Ebben az esetben $A_{1} C = B_{1} C$ , és a párhuzamos szelők tételének megfordítása alapján $A_{1} B_{1}$ is párhuzamos $A B$ -v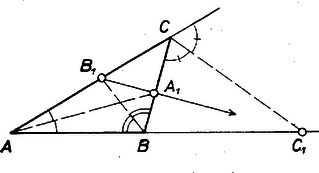el.

Legyen ezután a külső szögfelező és az

A B

egyenes metszéspontja

C_{1}

. A Menelaosz-tétel megfordítása szerint

A_{1}

B_{1}

C_{1}

akkor lesznek egy egyenesen, ha

\begin{matrix} \frac{A C_{1}}{C_{1} B} \cdot \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} = - 1. \end{matrix}

(1)

A külső szögfelező osztási arányára vonatkozó tétel szerint

\begin{matrix} \frac{A C_{1}}{C_{1} B} = - \frac{b}{a}, \end{matrix}

míg a belső szögfelezőkre vonatkozó tétel alapján

\begin{matrix} \frac{B A_{1}}{A_{1} C} = \frac{c}{b}, illetve \frac{C B_{1}}{B_{1} A} = \frac{a}{c}, \end{matrix}

ahol

a

b

c

a háromszög megfelelő oldalai.
Ezután (1) bal oldala így alakul:

\begin{matrix} - \frac{b}{a} \cdot \frac{c}{b} \cdot \frac{a}{c} = - 1. \end{matrix}

tehát

A_{1}

B_{1}

C_{1}

egy egyenesen vannak. Ezzel a feladat állítását bebizonyítottuk.

Boncz András (Zalaegerszeg, Zrínyi M. Gimn., III. o. t.)