Feladat: F.2746 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Benczúr P. ,  Benkő D. ,  Boda Z. ,  Boncz A. ,  Harcos G. ,  Jakab T. ,  Kovács 113 Vera ,  Sági Z. ,  Stoyan R. 
Füzet: 1990/október, 299 - 300. oldal  PDF  |  MathML 
Témakör(ök): Gráfok összefüggősége, Teljesgráfok, Fagráfok, erdők, faváz, Feladat
Hivatkozás(ok):Feladatok: 1989/május: F.2746

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladatban szereplő játéknak igazából csak n≥3-ra van értelme, így csak ezzel az esettel foglalkozunk. (n=1, 2-re senki sem veszít, tehát a játék "döntetlen''.) Azt állítjuk, hogy n≥3 esetén az veszít, akinek az n-edik élt kell kiszíneznie, azaz páros n-re A, páratlanra B nye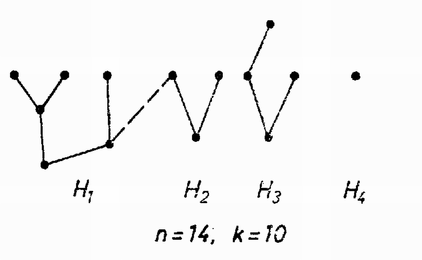r.

 
 

Ismeretes, hogy egy n-szögpontú, n élű gráfban van kör, tehát az n-edik él kiszínezése után biztosan lesz kör a piros színű élekből. Állításunk bizonyításához így elég azt belátni, hogy ha k<n, akkor az a játékos, aki a k-adik élt színezi, ezt meg tudja úgy tenni, hogy ő ne hozzon létre piros élekből álló kört. Tekintsük ugyanis azt a Gk-1 gráfot, amit az eddig kiszínezett k-1 él alkot az n ponton. Mivel k<n, ezért Gk-1 n-szögpontú, k-1<n-1 élű gráf, s ismeretes, hogy egy ilyen gráf nem lehet összefüggő. Ez azt jelenti, hogy szétbomlik kettő vagy több olyan összefüggő H1,H2,...,He részre, amelyek között nem fut él (l. ábra). Játékosunknak nem kell mást tennie, mint H1 valamely pontját és H2 valamely pontját egy piros éllel összekötni. Ha Gk-1-ben nem volt kör, akkor továbbra sem lesz (piros) kör, hiszen ehhez fel kellene használni az újonnan behúzott élt. De akkor ennek a körnek még egy élt is kellene tartalmaznia H1 és H2 között, ilyen pedig nincs. Ezzel beláttuk, hogy ha egy játékosnak csak a k(<n) sorszámra kell csak élt színeznie, akkor el tudja kerülni, hogy (piros) kört hozzon létre. Az a játékos viszont, akinek az n-edik él jut, ezt már nem tudja elkerülni. Ezzel állításunkat beláttuk.
 

Megjegyzés. A bizonyítás során felhasznált két gráfelméleti tétel röviden így fogalmazható:
1. Egy n-pontú összefüggő gráfnak legalább n-1 éle van.
2. Egy n-pontú körmentes gráfnak legföljebb n-1 éle van.
 

(Az elsőből következik, hogy egy n-pontú, k-1(<n-1) élű gráf nem összefüggő, s így több összefüggő részre esik szét. A másodikból következik, hogy egy n-pontú, n élű gráf nem lehet körmentes, azaz tartalmaz kört.)
Mindkét tétel egyszerűen következik abból a nevezetes gráfelméleti tényből, hogy egy n-pontú összefüggő körmentes gráfnak (fának) n-1 éle van. (Lásd pl. Hajnal I. ‐ dr. Nemetz T. ‐ dr. Pintér L.: Matematika III., B-fakultációs tankönyv 415‐416. old.) Egy összefüggő gráfból ugyanis mindig el lehet jutni élek elhagyásával egy összefüggő, körmentes gráfhoz. (Ha egy kör valamely élét elhagyjuk, ez nem "rontja el'' az összefüggőséget.) Másrészt egy körmentes gráfban ‐ ha nem összefüggő ‐ különböző összefüggő részei közötti él behúzásával eggyel csökkenthető az összefüggő részek száma, s így, ha l összefüggő részből áll, l-1 él behúzásával összefüggő, körmentes gráffá tehető (l. ábra). Ezzel mindkét állítást beláttuk.