Kezdőlap


Feladat:	F.2741	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Antos A. , Benczúr P. , Benkő Dávid , Boda Z. , Csirik J. , Hausel T. , Kovács T. , Lois L. , Mezei J. , Oláh G. , Peták Attila , Schultz J. , Siklér F. , Sustik M. , Újváry-Menyhárt Zoltán , Weisz Cs.
Füzet:	1989/december, 446 - 449. oldal		PDF \| MathML
Témakör(ök):	Exponenciális egyenlőtlenségek, Függvények, Sokszögek súlypontjának koordinátái, Egyéb ponthalmazok a koordinátasíkon, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1989/április: F.2741

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Rögzítsük először pl. $c$ értékét és keressük a $16^{a} + 16^{b} + 16^{c}$ kifejezés maximumát e rögzített $c$ mellett. Feltételeink szerint $a ≧ \frac{1}{4}$ , $b = 1 - a - c ≧ \frac{1}{4}$ . Mivel $16^{c}$ értéke ilyenkor szintén rögzített, ezért a $16^{a} + 16^{1 - c - a} = f (a)$ függvény maximumát kell megkeresnünk, ha $a ≧ \frac{1}{4}$ és $1 - a - c ≧ \frac{1}{4}$ , azaz ha $\frac{1}{4} ≦ a ≦ \frac{3}{4} - c$ . Az $a \mapsto f (a)$ függvény két konvex függvény: $16^{a}$ és $16^{1 - c} \cdot {(\frac{1}{16})}^{a}$ összege, így maga is konvex. Maximumát tehát az intervallum egyik (esetleg mindkét) végén veszi föl: $a = \frac{1}{4}$ vagy $a = \frac{3}{4} - c$ esetén. Utóbbi esetben $b = 1 - a - c = \frac{1}{4}$ tehát az $f (a)$ függvény, s így a $16^{a} + 16^{b} + 16^{c}$ kifejezés is, rögzített $c$ és a feladat feltételei mellett, akkor maximális, ha $a$ és $b$ valamelyike $\frac{1}{4}$ . Minthogy a kifejezés és a feladat feltételei teljesen szimmetrikusak, feltehetjük, hogy $a = \frac{1}{4}$ . Ha most $a = \frac{1}{4}$ -et rögzítjük, és a fenti gondolatmenetet újra alkalmazzuk, azt kapjuk, hogy a $16^{a} + 16^{b} + 16^{c}$ kifejezés akkor maximális, ha $b$ és $c$ egyikének értéke is $\frac{1}{4}$ , s ekkor a másik értéke $\frac{1}{2}$ . Azt kaptuk tehát, hogy ha $a + b + c = 1$ , $a$ , $b$ , $c ≧ \frac{1}{4}$ , akkor $16^{a} + 16^{b} + 16^{c} ≦ 16^{\frac{1}{4}} + 16^{\frac{1}{4}} + 16^{\frac{1}{2}} = 8$ , s ez éppen a feladat állítása.
$($ Egyenlőség pontosan akkor van, ha $a$ , $b$ , $c$ közül kettő értéke $\frac{1}{4}$ , a harmadiké $\frac{1}{2} .)$

Peták Attila (Bp., Berzsenyi D. Gimn., IV. o. t.)

II. megoldás: Ábrázoljuk az

x \mapsto 16^{x} = y

függvényt az (

x; y

) koordinátasíkon, és tekintsük a függvény grafikonjának a következő három pontját:

A = (a, 16^{a})

B = (b, 16^{b})

C = (c, 16^{c})

. A feltételek szerint

a

b

c ≧ \frac{1}{4}

és

a + b + c = 1

, így

a = 1 - b - c ≦ \frac{1}{2}

b ≦ \frac{1}{2}

c ≦ \frac{1}{2}

is teljesül. Tekintsük tehát a grafikon

P = (\frac{1}{4}; 16^{\frac{1}{4}}) = (\frac{1}{4}; 2)

és

Q = (\frac{1}{2}; 16^{\frac{1}{2}}) = (\frac{1}{2}; 4)

pontját.

1. ábra

Minthogy az

x \mapsto 16^{x}

függvény konvex, ezért az

A B C

háromszög teljes egészében abban a tartományban van, amelyet a

P Q

egyenes szakasz és a

P

és

Q

közötti grafikon határol (Az 1. ábrán satírozva van).
Nézzük most az

A B C

háromszög

S (\frac{a + b + c}{3}; \frac{16^{a} + 16^{b} + 16^{c}}{3}) = = (\frac{1}{3}; \frac{1}{3} (16^{a} + 16^{b} + 16^{c}))

súlypontját.Ez az

A B C

háromszög belsejében van, így szintén a satírozott részbe esik. Másrészt rajta van az

x = \frac{1}{3}

egyenesen. Ennek az egyenesnek a

P Q

-val és a függvénygrafikonnal alkotott metszéspontjai közé eső szakasza van a tartományban. Az egyenes a grafikont az

(\frac{1}{3}; 16^{\frac{1}{3}})

pontban, a

P Q

szakaszt annak

P

-hez közelebbi harmadolópontjában, az

(\frac{1}{3}; \frac{8}{3})

pontban metszi.
Így

\frac{1}{3} (16^{a} + 16^{b} + 16^{c})

értéke az adott feltételek

(\frac{1}{4} ≦ a b, c ≦ \frac{1}{2}, a + b + c = 1)

mellett

16^{\frac{1}{3}}

és

\frac{8}{3}

közé esik. Hárommal szorozva:

\begin{matrix} 3 \cdot 16^{\frac{1}{3}} ≦ 16^{a} + 16^{b} + 16^{c} ≦ 8. \end{matrix}

A második egyenlőtlenség éppen a feladat állítása.

Megjegyzés: Ez utóbbi megoldás általánosítható: Ha

f

konvex függvény,

n

természetes szám,

A

valós,

α = \frac{A}{n}

a_{1} + a_{2} + ... + a_{n} = A

és a

a_{1}, a_{2}, ..., a_{n} ≧ α

, akkor az

f (a_{1}) + f (a_{2}) + ... + f (a_{n})

függvény értéke akkor maximális, ha az

n

a_{i}

közül

(n - 1)

-nek az értéke

α

(az

n

-edik értéke pedig

A - (n - 1) α

.) A bizonyítás a 2. megoldáshoz hasonlóan történik: tekintjük az

A_{1} A_{2} ... A_{n}

(konvex)

n

-szöget, ahol

A_{i} = (a_{i} f (a_{i}))

, majd ennek

S (\frac{A}{n}; \frac{f (a_{1}) + ... + f (a_{n})}{n})

súlypontját. Az egyetlen különbség az, hogy a háromszög súlypontjáról tudjuk, hogy a háromszög belsejében van, a konvex

n

-szög esetében ezt bizonyítani kell (és lehet). A súlypont tehát megint egy függőleges egyenesen, az

x = \frac{A}{n}

egyenesen mozoghat, s ennek ,,legmagasabb'' pontja éppen a

P (α, f (α))

és

Q (A - (n - 1) α; f (A - (n - 1) α))

pontok közötti szakasz

P

-hez legközelebbi ,,

n

-edelő'' pontja. Ennek ordinátája éppen

\frac{1}{n} ((n - 1) f (α) + f (A - (n - 1) α),

ez tehát az

\frac{1}{n} \cdot \sum_{i - 1}^{n} f (a_{i})

kifejezés maximuma.

III. megoldás: A feladat még tovább is általánosítható: legyen adva az

f

konvex függvény, valamint az

α_{1} ≦ α_{2} ≦ ... ≦ α_{n - 1} ≦ α_{n}

számok, továbbá legyen

A ≧ \sum_{i = 1}^{n} α_{i}

. Ha

a_{1}, a_{2}, ..., a_{n}

olyan számok, amelyekre

a_{1} ≧ α_{1}

a_{2} ≧ α_{2}, ..., a_{n} ≧ α_{n}

és

a_{1} + a_{2} + ... + a_{n} = A

, akkor

\begin{matrix} f (a_{1}) + f (a_{2}) + ... + f (a_{n}) ≦ f (α_{1}) + f (α_{2}) + ... + f (A - \sum_{1}^{n - 1} α_{i}) . \end{matrix}

(1)

Változtassuk

a_{1}

értékét

a'_{1} = α_{1}

-re,

a_{n}

értékét pedig úgy módosítjuk, hogy az

a_{i}

-k összege továbbra is

A

maradjon:

a'_{n} = a_{n} + a_{1} - α_{1}

. Tudjuk, hogy

α_{1} ≦ a_{1}

és

α_{1} ≦ α_{n} ≦ a_{n}

. Másrészt

a'_{n} ≧ a_{n}

(hiszen

a_{1} - α_{1} ≧ 0

) és

a'_{n} ≧ a_{1}

(ugyanis

a_{n} - α_{1} ≧ α_{n} - α_{1} ≧ 0

).
Tehát

\begin{matrix} a'_{1} = α_{1} ≦ a_{1} a_{n} ≦ {a'}_{n} = a_{n} + a_{1} - α_{1} . \end{matrix}

Végül

a_{1} + a_{n} = a'_{1} + a'_{n}

. A két kapott feltételből már következik, hogy

\begin{matrix} f (a_{1}) + f (a_{n}) ≦ f (a'_{n}) + f (a'_{n}) . \end{matrix}

(2)

Tekintsük ugyanis az

A (a_{1}, f (a_{1}))

B (a_{n}, f (a_{n}))

A' (a'_{1}, f (a'_{1}))

B' (a'_{n}, f (a'_{n}))

, pontokat valamint az

A B

A' B'

szakaszokat. Előbbi felezőpontja legyen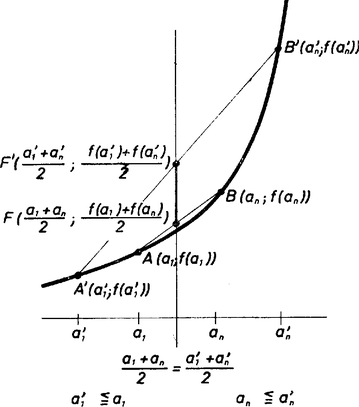

F

, utóbbié

F'

; nyilván

\begin{matrix} F = (\frac{a_{1} + a_{n}}{2}; \frac{f (a_{1}) + f (a_{n})}{2}) és F' = (\frac{a'_{1} + a'_{n}}{2}; \frac{f (a'_{1}) + f (a'_{n})}{2}) . \end{matrix}

2. ábra

Mivel

a_{1} + a_{n} = a'_{1} + a'_{n}

, a két felezőpont abszcisszája egyenlő. Másrészt

f

konvexitása és az

a'_{1} ≦ a_{1}

a_{n} ≦ {a'}_{n}

feltétel miatt az

\bar{A B}

szakasz teljesen az

\bar{A' B'}

szakasz alatt helyezkedik el. (l. a 2. ábrát), így az

\bar{A B}

szakasz

F

felezőpontjának ordinátája is kisebb az

\bar{A' B'}

szakasz

F'

felezőpontjának ordinátájánál. Ebből pedig éppen (2) következik.
Ezzel beláttuk, hogy

\begin{matrix} f (a_{1}) + f (a_{2}) + ... + f (a_{n}) ≦ f (α_{1}) + f (a_{2}) + ... + f (a_{n - 1} + f (a'_{n}) . \end{matrix}

Továbbra is fennáll

a_{2} ≧ α_{2}, a_{3} ≧ α_{3}, ..., a_{n}' ≧ α_{n}

és

a_{2} + ... + a_{n - 1} + a'_{n} = A - α_{1}

, ezzel a fenti gondolatmenet (

a_{2}, a'_{n}

)-re, majd (

a_{3}, a'_{n}

)-re stb. is megismételhető; (

n - 1

)-szeri ismétlés után megkapjuk (1)-et.
Benkő Dávid (Bp., Móricz Zs. Gimn., IV. o. t.)