Kezdőlap


Feladat:	F.2724	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Balogh József , Benkő Dávid , Tokodi Tamás
Füzet:	1990/január, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Halmazok számossága, Mátrixok, Feladat
Hivatkozás(ok):	Feladatok: 1989/január: F.2724

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük fel, hogy egy $m \times m$ -es táblázatot sikerült kitöltenünk úgy, hogy a sor- és az oszlopösszegek között nincsenek egyenlők. Ha $s_{i}$ és $o_{j}$ jelöli az elemek összegét az $i$ -edik sorban és a $j$ -edik oszlopban, akkor feltevésünk szerint az ${s_{i} : i = 1, 2, ..., m} \cap {o_{j} : j = 1, 2, ..., m}$ halmazt a $(2 m + 1)$ -elemű $[- m, m]$ halmazból kapjuk egy elem elhagyásával. Mivel ennek abszolút értéke legfeljebb $m$ , ezért az összegek abszolút értékének összegére:

\begin{matrix} A = \sum_{i = 1}^{m} | s_{i} | + \sum_{j = 1}^{m} | o_{j} | ≧ (\sum_{i = - m}^{m} | i |) - m = m^{2} . \end{matrix}

(1)

[- m, m]

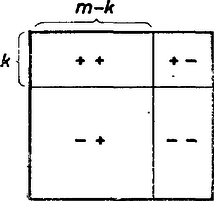halmaznak pontosan egy eleme nincs ott az összegek között, ezért található

m

darab nem negatív összeg úgy, hogy a további

m

darab összeg nem pozitív. Sorok és oszlopok cseréjével rendezzük át a táblázatot úgy, hogy az első

k

sor és az első

(m - k)

oszlop adja ezeket a nemnegatív összegeket. Eközben a sor- és oszlopösszegek nyilván nem változnak. Ekkor

\begin{matrix} A = \sum_{i = 1}^{m} | s_{i} | + \sum_{j = 1}^{m} | o_{j} | = (s_{1} + ... + s_{k}) - (s_{k + 1} + ... + s_{m}) + \\ + (o_{1} + ... + o_{m - k}) - (o_{m - k + 1} + ... + o_{m}) . \end{matrix}

A fenti összegben a "

+ +

'' típusú elemeket kétszer adtuk össze, a "

‐

'' típusúakat kétszer vontuk ki, míg a "vegyes'' "

+ -

'', illetve "

- +

'' típusú elemek kiesnek. Így

A

akkor a legnagyobb, ha a "

+ +

'' típusú elemek értéke 1, a "

- -

'' típusúaké pedig

- 1

, tehát

\begin{matrix} A ≦ 4 k (m - k) . \end{matrix}

(2)

(1)-et és (2)-t összevetve

\begin{matrix} m^{2} ≦ 4 k (m - k), \end{matrix}

azaz

{(m - 2 k)}^{2} ≦ 0

, ami nem lehetséges, ha

m

páratlan. Ezzel a bizonyítást befejeztük.

Megjegyzés. A Gy. 2529. gyakorlat szerint páros oldalú táblázat kitölthető úgy, hogy a sor- és oszlopösszegek között ne legyenek egyenlők.