| Feladat: | F.2721 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Antos András , Bakos Tibor | ||
| Füzet: | 1989/november, 372 - 374. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Ponthalmazok, Egyenlő szárú háromszögek geometriája, Indirekt bizonyítási mód, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1988/december: F.2721 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat állítását indirekt módon bizonyítjuk. Tegyük fel, hogy a hét pont közül bármelyik három egyenlő szárú háromszöget alkot. Legyen közülük kettő és . A további öt pont mindegyike nem lehet felezőmerőlegesén, mert akkor ezek közül három nem alkotna (egyenlő szárú) háromszöget. Ezért van olyan pont, amely -val és -vel úgy alkot egyenlő szárú háromszöget, hogy p1. . Tekintsünk egy ilyen háromszöget, és vizsgáljuk meg, hol helyezkedhet el a további négy pont. Ha egy további pont helyzetét az és pontokhoz viszonyítva nézzük, megállapíthatjuk, hogy rajta van az középpontú, sugarú, vagy a középpontú sugarú körön, vagy felezőmerőlegesén, hiszen az háromszög egyenlő szárú. Jelöljük e két kör és a felezőmerőleges pontjainak a halmazát -vel. Hasonlóan értelmezzük a és a halmazokat. Feltevésünk szerint a további négy pont mindegyike az pontok közül bármelyik kettővel egyenlő szárú háromszöget alkot. Ezért mind a négy pont eleme lesz a , és halmazok közös részének.  Az ábrán megrajzoltuk a szóban forgó halmazokat, és a , , , , , pontokból álló metszetüket. Mivel ezek közül , , , és egy egyenesen van, akárhogyan választunk ki , , mellé további négy pontot a lehetségesek közül, a kapott hét pont között mindig lesz legalább három, amely egy egyenesre esik, és ezért nem alkot (egyenlő szárú) háromszöget. Ez ellentmond indirekt feltevésünknek. Így a feladat állítása igaz. Antos András (Budapest, Árpád Gimn., III. o. t.) dolgozata alapján Megjegyzések. 1. A fenti módszerrel ‐ igaz, némi többletmunka árán ‐ beláthatjuk, hogy ha a sík hat pontja közül bármelyik három egyenlő szárú háromszöget határoz meg, akkor ezek egy szabályos ötszög csúcsai és középpontja. 2. Ennek az állításnak a közölt módszertől eltérő bizonyítása megtalálható Skljarszkij‐Csencov‐Jaglom: Válogatott feladatok és tételek az elemi matematika köréből (Geometria I.) c. könyvének 90 ‐ 94. oldalán 3. Erdős professzor úr a feladatot az American Math. Monthly c. folyóiratban közölte évekkel ezelőtt. 4. A térben viszont kijelölhető olyan pont, amely kielégíti a feltételeket. A teljesség igénye nélkül mutatunk példákat. a) Egy háromoldalú, egyenlő élű hasáb csúcsa és a köréje írt gömb középpontja (2. ábra). 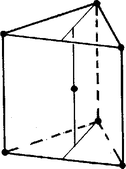 b) Egy szabályos síkötszög csúcsai, hozzájuk véve az középpontjában az síkjára állított tengelyének két, az -re tükrös pontját (ötoldalú szabályos bipiramis) (3. ábra). 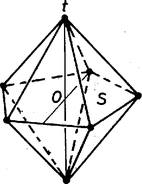 c) Az előbbi ötszöghöz egy pontját vesszük hozzá (lehet maga is) továbbá az ötszög csúcsain átmenő, körüli gömbnek -vel való metszéspontjai közül az egyiket (4. ábra). 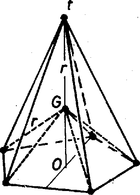 Továbbiakat úgy lehetne keresni, hogy a fenti körök helyett gömböket veszünk és felező merőleges síkokat. A fenti együttesekből egy pontot (pl. ötszögcsúcsot) elhagyva pontos együtteseket kapunk. Elmondunk egy olyat is, amely nem kapható meg elhagyással vagy ötszög helyett négyzetet véve. Egy -os szögű rombusz és a rövidebb átlójának végpontjaiban a síkjára emelt merőlegeseknek azok az , pontjai, amelyekre (vagyis négyzet). A példákat a Gy. 596. megoldói gyűjtötték, a megoldás és megjegyzései 1960.okt.‐nov. számainkban jelentek meg. |