Kezdőlap


Feladat:	F.2715	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1989/szeptember, 257 - 258. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Beírt gömb, Elsőfokú (és arra visszavezethető) egyenletrendszerek, Tetraéderek, Feladat
Hivatkozás(ok):	Feladatok: 1988/november: F.2715

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Érintse a tetraéder beírt gömbje a $B C D$ lapot a $G$ , az $A C D$ lapot a $H$ pontban. Használjuk az ábra további jelöléseit is. Mivel egy külső pontból a gömbhöz húzott érintőszakaszok egyenlőek,

\begin{matrix} A E = A F és B E = B F . \end{matrix}

Ezért az

A B E

és

A B F

háromszögek egybevágók, hiszen oldalaik páronként egyenlők. Ebből következik, hogy

A E B ∢ = A F B ∢

; ezeket a szögeket az ábrán

α

-val jelöltük.
Ugyanígy megmutathatók a következő egybevágóságok:

\begin{matrix} B C E ▵ ≅ B C G ▵ \\ A C E ▵ ≅ A C H ▵ \\ A D F ▵ ≅ A D H ▵ \\ C D G ▵ ≅ C D H ▵ \\ B D F ▵ ≅ B D G ▵ \end{matrix}

és ezekből az egybevágóságokból adódik az ábrán azonos betűvel jelölt szögek egyenlősége.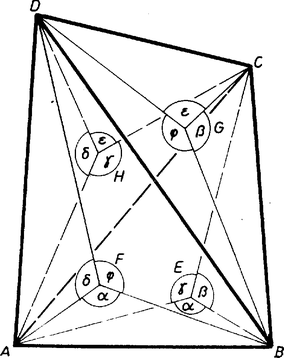

E, F, G

és

H

érintési pontok mindegyike a tetraéder egy-egy lapjának belső pontja, ezért

\begin{matrix} α + β + γ = 2 π \\ β + φ + ε = 2 π \\ γ + δ + ε = 2 π \\ α + δ + φ = 2 π . \end{matrix}

Az első két egyenletből

\begin{matrix} α + γ = φ + ε, \end{matrix}

a másik két egyenletből pedig

\begin{matrix} α + φ = γ + ε . \end{matrix}

E két utóbbi egyenletből

\begin{matrix} γ = φ, azaz A E C ∢ = B F D ∢ . \end{matrix}

Ezt kellett bizonyítanunk.