Kezdőlap


Feladat:	F.2709	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Balogh 171 J. , Csilling Á. , Csirik J. , Fleiner T. , Hausel T. , Hídvégi Z. , Tokodi I.
Füzet:	1989/április, 159 - 160. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Háromszögek nevezetes tételei, Gömb és részei, Tetraéderek, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1988/október: F.2709

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mérjünk fel a $D A$ félegyenesre $D$ -ből kiindulva egy olyan szakaszt; amelynek a hossza $D B \cdot D C$ ; legyen ennek a szakasznak a másik végpontja $P$ . Hasonlóan kapjuk a $D Q$ , ill. $D R$ szakaszokat, amelyek hossza $D A \cdot D C$ , ill. $D A \cdot D B$ .
Az $A B D$ háromszög hasonló a $Q P D$ háromszöghöz, hiszen megegyezik két oldalpárjuk aránya és a közbezárt szög. Ezért

\begin{matrix} \frac{Q P}{A B} = \frac{D P}{D B}, azaz \frac{Q P}{A B} = \frac{D B \cdot D C}{D B}, \end{matrix}

így

\begin{matrix} Q P = A B \cdot D C . \end{matrix}

Hasonlóan kapjuk, hogy

R Q = B C \cdot D A

és

P R = C A \cdot D B

Könnyen láthatjuk, hogy a

P Q R

háromszög valóban létezik, hiszen csúcsai rendre a nem egysíkú

D A, D B, D C

félegyeneseken lévő,

D

-től különböző pontok. Tudjuk, hogy az

A B C

háromszög szabályos, vagyis

A B = B C = C A

. Ha az

A B

szakasz hossza

d

, akkor a

P Q R

háromszög oldalai

d \cdot D A, d \cdot D B, d \cdot D C

. A

P Q R

háromszög

d

-szeres kicsinyítésével tehát olyan háromszöget kapunk, amelynek oldalai éppen

D A, B C, D C

nagyságúak.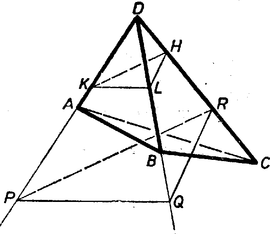

II. megoldás. Vegyünk fel egy olyan gömböt, amely illeszkedik az

A, B, C

pontokra, és amelynek a

D

csúcs külső pontja. (Ilyen gömb biztosan létezik.) Legyen a

D A, D B

és

D C

élek másik közös pontja a gömbbel

K, L

és

H

. Az

A, B, D

pontok síkja a gömböt egy körben metszi, tehát az

A B L K

négyszög húrnégyszög. A húrnégyszögek tétele szerint

D K L ∢ = A B L ∢

. Emiatt a

D A B

háromszög hasonló a

D L K

háromszöghöz, hiszen a

D

-nél lévő szögük is azonos. Ugyanilyen meggondolás alapján a

D B C

háromszög hasonló

D H L

-hez, a

D C A

háromszög pedig

D K H

-hoz.
Az első két háromszögpár hasonlóságából

\begin{matrix} \frac{K L}{D L} = \frac{B A}{D A} és \frac{H L}{D L} = \frac{B C}{D C} . \end{matrix}

E két egyenlet hányadosa:

\begin{matrix} \frac{K L}{H L} = \frac{B A \cdot D C}{D A \cdot B C} = \frac{D C}{D A}; \end{matrix}

(1)

(közben felhasználtuk, hogy

B A = B C

.) Ugyanígy kapjuk, hogy

\begin{matrix} \frac{H L}{K H} = \frac{D A}{D B} . \end{matrix}

(2)

(1) és (2) azt jelenti, hogy a biztosan létező

K L H

háromszög hasonló ahhoz a háromszöghöz, amelynek oldalai

D A, D B

és

D C