Feladat: F.2708 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Csirik János 
Füzet: 1989/március, 110 - 112. oldal  PDF  |  MathML 
Témakör(ök): Sokszög lefedések, Szabályos sokszögek geometriája, Feladat
Hivatkozás(ok):Feladatok: 1988/október: F.2708

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az n oldalú szabályos sokszög egy szöge n-2n⋅180∘. Ezért egy csúcsban nem találkozhat három, a feldaraboláskor keletkező szabályos sokszög, mert már a legkisebb szögű szabályos sokszög egy szögének háromszorosa is 180∘. Így csak azokat a lehetőségeket kell vizsgálnunk, amikor a felbontandó szabályos sokszög egy-egy szögét a feldaraboláskor keletkezett egy vagy két sokszög szöge fedi le.

 
 
1. ábra
 

Nézzük először azt az esetet, amikor a szabályos sokszög egy szögét egyetlen, vele egyenlő nagyságú szög takarja le. A feldaraboláskor keletkező ugyanolyan szögű szabályos sokszög oldala nyilván kisebb lesz, mint az eredeti sokszög oldala, ezért, amint azt az 1. ábrán láthatjuk, egy ilyen sokszög mellett keletkezik egy 2n⋅180∘ nagyságú szög is, amelyet szabályos sokszögek szögeivel kell kitölteni. Ha n=3, illetve n=4, akkor 2n⋅180∘ értéke 120∘, illetve 90∘ lesz, és mint a 2. és 3. ábrán láthatjuk, a feldarabolás lehetséges (többféleképpen is). Az n=5 esetben 2n⋅180∘=72∘, ami nem tölthető ki szabályos sokszögek szögeivel. Ugyanez a helyzet, ha n>6, akkor ugyanis 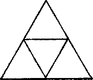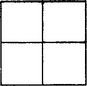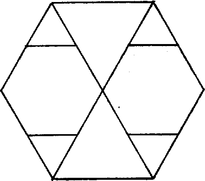2n⋅180∘<60∘.
 
 
2. ábra
 

 
 
3. ábra
 

 
 
4. ábra
 

Az n=6 esetben például a 4. ábra szerint történhet a feldarabolás. Ha az eljárást az O csúcsot tartalmazó hatszögekre folytatjuk, további megoldásokhoz jutunk. Ebben az esetben az A csúcsnál levő szöget egyetlen új sokszög egyetlen szöge fedi le, a B csúcsnál levő szöget pedig kettő.
Legutóbbi megoldásunkkal tehát áttérünk arra az esetre, amikor a sokszög egy csúcsánál két szabályos háromszög találkozik. A sokszög szöge így 120∘, ez tehát a szabályos hatszög, ami nyilván felbontható (többféleképpen is) szabályos háromszögekre.
Egy csúcsnál szabályos háromszög és négyzet is találkozhat. Ekkor a szabályos sokszög szöge 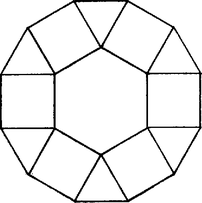60∘+90∘=150∘, és
n-2n⋅180∘=150∘alapjánn=12.

 
 
5. ábra
 

Az 5. ábrán láthatjuk, hogy a szabályos 12-szög valóban összerakható 6 darab szabályos háromszögből, 6 darab négyzetből és egy szabályos hatszögből.
Már csak azt kell megvizsgálnunk, hogy egy csúcsban találkozhat-e egy szabályos háromszög és egy szabályos ötszög.
Ekkor a sokszög egy szöge 60∘+108∘=168∘, és
n-2n⋅180∘=168∘alapjánn=30.

 
 
6. ábra
 

Ha most az ötszög és a 30-szög oldala egyenlő, akkor a 6. ábrán látható 84∘-os szög nem fedhető le szabályos sokszögek szögeivel. Ha pedig az ötszög oldala kisebb, mint a 30-szögé, akkor az 1.ábrán vázolt esethez hasonlóan az ötszög mellett keletkezne egy 25⋅180∘=72∘-os szög, amely nem fedhető le szabályos sokszögek szögeivel.
A feladat követelményeinek tehát a 3, 4, 6 és 12 oldalú szabályos sokszög felel meg.
 

 Csirik János (Szeged, Ságvári E. Gyak. Gimn., III. o. t.)
 dolgozata alapján