Feladat: F.2696 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Baboss Cs. ,  Benczúr Péter ,  Benkő D. ,  Csordás Z. ,  Farkas J. ,  Hadnagy Éva ,  Keleti T. ,  Kodaj B. ,  Lois L. ,  Mezei J. ,  Mohai Zs. ,  Peták A. ,  Siklér F. ,  Tóth 702 P. 
Füzet: 1988/december, 445 - 446. oldal  PDF  |  MathML 
Témakör(ök): Síkra vonatkozó tükrözés, Mértani helyek, Térelemek és részeik, Gömb és részei, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):Feladatok: 1988/május: F.2696

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük egy ilyen gömb középpontját O-val. Ha speciálisan A egybeesik B-vel, akkor minden O gömbközéppont egyenlő távolságra van A-tól és S-től. Az ilyen tulajdonságú pontok halmaza olyan forgási paraboloidfelület, amelynek tengelye merőleges az S síkra. Ezt a paraboloidot úgy is megkaphatjuk, hogy egy A-n átmenő, S-re merőleges síkban ‐ melynek S-sel való metszete m ‐ megkeressük az A-tól és m-től egyenlő távolságra lévő pontok mértani helyét. Ez egy parabola, amelynek tengelye körüli megforgatásával nyerhetjük az előbb említett paraboloidot. A paraboloidfelület minden pontja nyilván egy olyan gömb középpontja lehet, amely átmegy A-n és érinti az S síko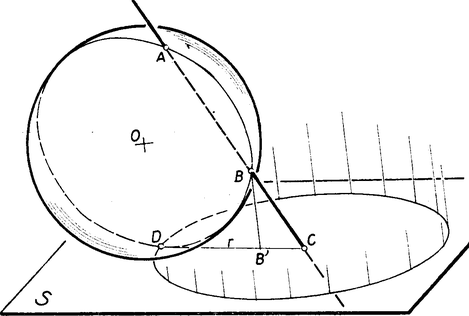t.

 
 

Ha az AB szakasz párhuzamos S-sel, akkor a fenti gondolatmenet mind A-ra, mind B-re elmondható, s a gömbközéppontok mértani helye a két egybevágó forgási paraboloidfelület metszete lesz, ami parabola.
Ezt a tényt egyszerűbben is beláthatjuk. A két paraboloid nyilván szimmetrikus az AB szakasz felező merőleges síkjára. A keresett gömbközéppontok ebben a síkban vannak, a mértani hely tehát akármelyik előbbi paraboloidfelület és a felező merőleges sík metszete, vagyis parabola. Nyilván a parabola minden pontja megfelel.
Tegyük fel ezután, hogy AB egyenes nem párhuzamos S-sel, jelöljük a közös pontjukat C-vel. Legyen O egy megfelelő gömb középpontja, ennek S-re való vetülete D. Az S sík D-ben érinti a gömböt, ezért a C pontnak az A és B pontokon átmenő, O középpontú körre vonatkozó hatványa:
CD2=CA⋅CB.
Ez azt jelenti, hogy CD állandó, tehát a D érintési pontok mértani helye egy r=CA⋅CB sugarú kör. Ennek a körnek minden pontjához tartozik egy olyan O középpontú gömb, amely átmegy A-n és B-n. A gömb középpontja egyfelől rajta van a D pontokban S-re állított merőleges egyenesek valamelyikén, tehát egy C körül r sugárral rajzolt kör alapú henger felületén, másfelől rajta van az AB szakasz felező merőleges síkján. Ezért a keresett mértani hely ebben az esetben egy hengerfelület és egy sík metszete, tehát ellipszis. (Speciálisan, a síkmetszet kör lesz, ha AB merőleges S-re.) Világos, hogy az ellipszis minden pontja megfelelő gömbközéppont.