Kezdőlap


Feladat:	F.2695	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1989/január, 11 - 14. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos és egyéb hasonlósági transzformációk, Körülírt kör középpontja, Síkgeometriai szerkesztések, Feladat
Hivatkozás(ok):	Feladatok: 1988/május: F.2695

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelölje a háromszög csúcsait $A$ , $B$ , $C$ , a körök középpontját $P$ , $Q$ , $R$ . Nézzük a háromszög egyik oldalát. Az oldalt érintő két (különböző) kör érinti a háromszög további 1-1 oldalát is, így a két kör középpontja az oldal egyenesének ugyanabban a félsíkjában van, mint $A B C$ . Mivel a körök sugara egyenlő, a középpontjukat összekötő egyenes párhuzamos a kiszemelt oldallal. Ez mindegyik oldalra igaz, ezért a $P Q R$ háromszög hasonló az $A B C$ háromszöghöz. A három kör közös pontja a $P$ , $Q$ , $R$ pontoktól egyenlő távolságra van, ezért ez a pont a $P Q R$ háromszög köré írt körének a középpontja.
Ezután a feladatot úgy oldhatjuk meg, hogy szerkesztünk egy hasonló ábrát, és azt alkalmasan kicsinyítjük. Ezt a következőképpen tehetjük meg. Az $A B C$ háromszög mindegyik csúcsa köré a háromszög köré írt kör középpontján is átmenő (és így egyenlő sugarú) köröket rajzolunk. Sorra mindegyik körpárnak húzzuk meg azt a közös érintőjét, amelyik nem metszi a harmadik kört. A három érintő olyan háromszöget határoz meg, amelyik hasonló az $A B C$ háromszöghöz, és a három kör e háromszög oldalait a feladat követelményei szerint érinti. Tekintsük végül azt a hasonlósági transzformációt, amely ezt a háromszöget az $A B C$ háromszögbe viszi át. Ez a transzformáció a három kört olyan körökbe képezi le, amilyeneket szerkeszteni kell.

Megjegyzések: 1. Mivel az említett két háromszög "párhuzamosan'' hasonló, középpontosan is hasonló, így könnyű látni, hogy a hasonlóság centruma a belső szögfelezők metszéspontja. A megoldásban azért kellett két kör közös érintői közül a harmadik kört nem metszőt választani, mert az "oldal'' szót "szakasz'' értelemben használjuk, és a hat érintési pont így biztosan az oldalak egy-egy pontja lesz. Azt is látjuk, hogy a feladatnak mindig van megoldása.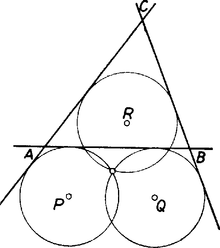

1. ábra

2. Ha a feladat szövegében "oldal'' helyett "oldalegyenes'' szerepel, a hasonló ábra készítésénél bármelyik két kör mindkét közös érintője számításba jön, és így az érintők 2‐3 különböző hasonló háromszöget határoznak meg. E 8 megoldás egyikét vázoltuk az 1. ábrán. Itt a

P

és

Q

középpontú kör nem az

A C

, illetve

B C

oldalt, hanem azok meghosszabbítását érinti. Ez esetben a hasonlóság centruma a

C

csúcshoz tartozó belső, és a másik két csúcshoz tartozó külső szögfelező közös pontja. Ha

A B C

derékszögű háromszög, akkor az előbbi 8 megoldáson kívül még úgy is szerkeszthetők a körök, hogy azok közül kettő érintkező legyen. E négy megoldás egyikét az 5. ábra mutatja.
3. Eredeti feladatunkhoz visszatérve felvetődik a kérdés, hogy a 2. pontban említett (általánosabb értelemben vett) megoldások között van-e még olyan, amelyiknél valamennyi érintési pont az oldalakra (vagy pedig azok meghosszabbítására) esik. A 2. és a 3. ábra mindenesetre azt mutatja, hogy ha az

A B C

háromszög szabályos, akkor legalább két megoldás lehetséges. A 3. ábrán vázolt esetben a hasonló ábra szerkesztésekor bármelyik két kör közös érintőjét úgy választhatjuk, hogy az messe a harmadik kört.

2. ábra

3. ábra

Megmutatjuk, hogy ha az

A B C

háromszög nem szabályos, akkor a feladatnak pontosan egy megoldása van, szabályos háromszög esetén pedig csak a fenti két megoldás létezik. Ehhez a 2. pontban szereplő eseteket egyenként meg kell vizsgálni. Állításunk könnyen belátható minden olyan esetben, amikor a háromszög megszerkesztéséhez felhasznált közös érintők valamelyike nem metszi az őt nem érintő harmadik kört; a részleteket az Olvasóra hagyjuk.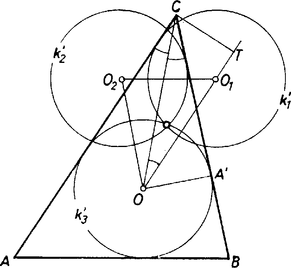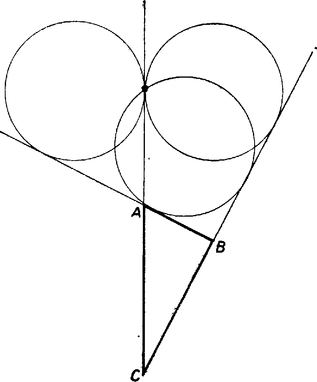

4. ábra

5. ábra

Tegyük fel viszont, hogy az

A B C

háromszöghöz található három, egy ponton átmenő, egyenlő sugarú

k_{1}, k_{2}

, ill.

k_{3}

kör úgy, hogy ezek rendre érintik az

A C

és

A B, B C

és

A B

, ill.

A C

és

B C

oldalakat, továbbá metszik a

B C, A C

, ill.

A B

oldalt. Feltehetjük, hogy például

B C \leq A C \leq A B

. Kicsinyítsük a

k_{i}

köröket

C

-ből úgy, hogy a kapott

k'_{1}

k'_{2}

k'_{3}

körök közül

k'_{3}

éppen az

A B C

háromszögbe írt kör legyen (4. ábra). Jelölje

k'_{1}

k'_{2}

, és

k'_{3}

középpontjait

O_{1}

O_{2}

és

O

;

C

-ből az

O O_{1}

egyenesre állított merőleges talppontja legyen

T

, végül jelöljük

A'

-vel azt a pontot, amelyben

k'_{3}

B C

oldalt érinti. Mivel

k'_{1}

érinti az

A C

oldalt, ezért

\begin{matrix} O O_{1} \leq O T . \end{matrix}

(1)

Mint azt már korábban láttuk, az

O_{1} O_{2} O

háromszög hasonló

A B C

-hez, a hasonlóság aránya pedig

\frac{r}{R}

, ahol

r

A B C

háromszögbe,

R

pedig a háromszög köré írható körnek a sugara. Így (a háromszög oldalait és szögeit a szokásos módon jelölve)

\begin{matrix} O O_{1} = \frac{r}{R} b . \end{matrix}

(2)

O T C

és az

O A' C

derékszögű háromszögek egybevágók, hiszen közös

O C

átfogójukon kívül egyik hegyesszögük

\frac{γ}{2}

; ezért

\begin{matrix} O T = C A' = \frac{1}{2} (a + b - c), \end{matrix}

(3)

(1), (2) és (3) alapján

\begin{matrix} \frac{r}{R} b \leq \frac{1}{2} (a + b - c), \end{matrix}

azaz (a háromszög területét

t

-vel jelölve)

\begin{matrix} \frac{a + b - c}{b} \geq \frac{2 r}{R} = \frac{4 t}{a + b + c} \cdot \frac{4 t}{a b c}, \\ a + b - c \geq \frac{16 t^{2}}{a c (a + b + c)} = \frac{(- a + b + c) (a - b + c) (a + b - c)}{a c}, \end{matrix}

így

\begin{matrix} a c \geq (a + (c - b)) \cdot (c + (b - a)) . \end{matrix}

Mivel feltevésünk szerint

c \geq b \geq a

, ezért a fenti egyenlőtlenségből

c - b = 0 = b - a

következik; az

A B C

háromszög tehát szabályos.