Feladat: F.2685 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Baboss Cs. ,  Balogh 171 József ,  Bíró 100 A. ,  Csirik J. ,  Fleiner T. ,  Keleti Tamás ,  Kodaj B. ,  Mezei J. ,  Pásztor G. ,  Peták A. ,  Szabó 668 T. ,  Tirpák E. ,  Tóth 02 P. 
Füzet: 1988/december, 442 - 443. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Indirekt bizonyítási mód, Tetraéderek, Feladat
Hivatkozás(ok):Feladatok: 1988/március: F.2685

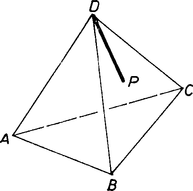
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Azt állítjuk, hogy egy tetraéder bármelyik belső pontjából legalább három él tompaszögben látszik. Azt is megmutatjuk, hogy ez az állítás nem élesíthető, ugyanis minden tetraédernek van olyan belső pontja, amelyből pontosan három él látszik tompaszögben.
a) Az első állítást a következőképpen láthatjuk be. Tekintsük a DP-re merőleges, P-n átmenő síkot. E sík által meghatározott egyik féltérben van a D pont. A másik féltérben van az A,B,C pontok közül legalább egy, különben P nem lehetne belső pont. Legyen ez a pont A; ekkor APD tompaszög. Ez a gondolatmenet D helyett bármelyik csúcsra alkalmazható, tehát mindegyik csúcsból indul ki olyan él, amely P-ből tompaszögben látszik. Ha a B és C csúcsból kiinduló ilyen tulajdonságú élek különbözők, akkor van három él, amely P-ből tompaszögben látszik. Ha ez a két él ugyanaz, akkor annyit tudunk, hogy AD és BC ‐ két szemközti él ‐ tompaszögben látszik P-ből.

 
 
1. ábra
 

Nézzük ezután a P-n átmenő, AP-re, ill. PD-re merőleges síkokat. (Az ábrát úgy készítettük, hogy az A,P,D pontok a rajz síkjában vannak, az említett merőleges síkokat pedig a rajz síkjával képezett metszésvonaluk szemlélteti.) Azok az X pontok, amelyekre APX és DPX egyaránt hegyesszög, abban a térrészben vannak, amelynek a rajz síkjára eső vetületét bevonalkáztuk. Mivel APD tompaszög, ez a térbeli tartomány a DP-n átmenő, a rajz síkjára merőleges síknak ugyanazon az oldalán van, mint az A pont. Ezért, ha B is és C is ebben a tartományban lenne, P nem lehetne belső pont. Ha pl. B nincs ebben a tartományban, akkor P-ből AB vagy BD tompaszögben látszik.
Ezzel az első állítást beláttuk.
b) A második állítás igazolásához fölhasználhatjuk azt az egyszerű tényt, hogy egy tetraédernek mindig van olyan csúcsa, amelybe futó élek közül bármelyik kettő hegyesszöget zár be. Ezt indirekt úton igazolhatjuk. Tegyük fel, hogy mindegyik csúcsnál van egy legalább 90∘-os szög. Mivel az egy csúcshoz illeszkedő három élszög közül bármelyik kettő összege nagyobb, mint a harmadik, minden csúcsnál 180∘-nál nagyobb a szögek összege. Mivel négy csúcs van, az összes lapon lévő szögek összege nagyobb lenne 4⋅180∘-nál, de ez ellentmondás, hiszen a négy háromszöglapon a szögek összege pontosan 4⋅180∘. Van tehát olyan csúcs, amelyhez illeszkedő élszögek mind hegyesszögek. Legyen ez a D csúcs. Ekkor D kívül esik az AB,BC,CA élekhez tartozó Thalész-gömbökön, így D-nek van olyan környezete is (egy D középpontú gömb), amely ezeken a gömbökön kívül helyezkedik el. Vegyünk ebből a környezetből egy olyan P pontot, amely a tetraédernek belső pontja. Az AB, BC, CA élek P-ből is hegyesszögben látszanak, másrészt az első állításunk szerint a másik három él tompaszögben látszik P-ből.
 

 Balogh 171 József (Szeged, Ságvári E. Gimn., II. o. t.) és
 Keleti Tamás (Bp., Fazekas M. Gyak. Gimn., IV. o. t.)
 dolgozata alapján
 
II. megoldás. Jelölje S a P-nél keletkező hat darab szög összegét. A P négy tetraéder közös csúcsa, ezek lapjain az élszögek összege
4⋅4π=16π=2S+4π+R,(1)
ahol R az ABCD tetraéder élei és a P-t a tetraéder csúcsaival összekötő szakaszok által bezárt szögek összege.
 
 
2.a ábra
 

 
 
2.b ábra
 

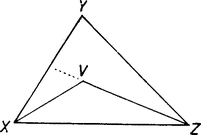Ismeretes, hogy egy triéder bármely két élszögének összege nagyobb a harmadiknál. Ennek ismételt alkalmazásával az XV+VZ<XY+YZ egyenlőtlenség (2. ábra) bizonyításához hasonlóan kapjuk, hogy
PDA∢+PDB∢<CDA∢+CDB∢.
Ugyanilyen becslés igaz a PD által felosztott D csúcsú triéder másik két szögpárjára is. A három egyenlőtlenséget összeadva azt kapjuk, hogy D-nél a tetraéder belsejében létrejövő három szög összege kisebb, mint a D-ben találkozó ABD, BCD és CAD tetraéderlapok D csúcsú szögeinek összege. Ugyanez a további három tetraédercsúcsnál is teljesül, és így R kisebb, mint az ABCD tetraéder élszögeinek összege, 4π. Ennek alapján (1)-ből
4π<S
következik. Így a hat darab P-csúcsú szög közül legalább három tompaszög, hiszen 2⋅π+4⋅π2=4π.