Kezdőlap


Feladat:	F.2667	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Hadnagy Éva , Peták A. , Tóth 702 P.
Füzet:	1988/május, 207 - 210. oldal		PDF \| MathML
Témakör(ök):	Forgatva nyújtás, Körök, Diszkusszió, Feladat
Hivatkozás(ok):	Feladatok: 1987/december: F.2667

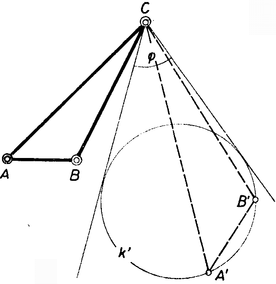
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Elegendő egy, a kívánt ábrához hasonló alakzatot szerkesztenünk, ezt ugyanis alkalmas hasonlósági transzformáció a megfelelő helyzetbe viszi. Rajzoljunk egy $C$ csúcsú $φ$ szögtartományt és egy ennek szárait érintő $k^{'}$ kört. Ha most a $k^{'}$ kerületén megszerkesztjük azokat az $A^{'}$ és $B'$ pontokat, amelyekre a $C A^{'} B^{'}$ és a $C A B$ alakzatok hasonlóak (1. ábra), akkor az a $C$ közepű forgatva nyújtás, amelyik $A^{'}$ -t az $A$ -ba viszi, a $B^{'}$ -t a $B$ -be, a $k^{'}$ kört pedig az $A$ és $B$ pontokon áthaladó $k$ körbe fogja vinni, és eközben $φ$ -vel egyenlő marad az a szög, amelyben a $k$ kör a $C$ pontból látszik, tehát $k$ egy megoldása a feladatnak.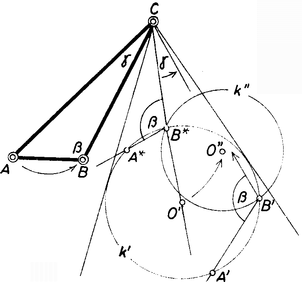

1.a ábra

1.b ábra

Ha a

C A^{'} B^{'}

és a

C A B

alakzatok hasonlók, akkor az

A^{'}

pontot egy

C

közepű,

A C B

szögű

F

forgatva nyújtás viszi a

B^{'}

pontba. (Az

1 / b

ábrán, ahol az

A, B

és

C

egy egyenesre esnek,

F

középpontos hasonlóság.) Az

F

így az

A^{'}

-n áthaladó

k^{'}

kört egy a

B^{'}

-n áthaladó

k^{''}

körbe viszi, ezért a

B^{'}

pontot a két kör,

k'

és

k^{''}

metszéspontjaként kapjuk, ha ez létrejön. Az

A^{'}

pontot ezután a

C B^{'}

-vel

C B A

szöget bezáró,

B^{'}

kezdőpontú félegyenes metszi ki a

k^{'}

körből (1.a. ábra).
A megoldások száma 0, 1 vagy 2 aszerint, hogy hány közös pontja van a

k^{'}

és a

k''

köröknek.
A két segédkör,

k^{'}

és

k^{''}

akkor és csak akkor metszi vagy érinti egymást, ha sugaraik összege legalább akkora, mint a középpontjaik távolsága. (A két kör nem tartalmazhatja egymást, mert

C

, a hasonlóság centruma mindkettejüknek külső pontja.) Jelölje a sugarakat

r^{'}

és

r^{''}

, a középpontokat pedig

O^{'}

és

O^{''}

. Ekkor

\begin{matrix} r^{'} & = O^{'} C \cdot sin \frac{φ}{2}, \\ r^{''} & = r^{'} \cdot \frac{B C}{A C}, \end{matrix}

O^{'} C O^{''}

és

A C B

alakzatok hasonlóságából pedig

\begin{matrix} O^{'} O^{''} = O^{'} C \cdot \frac{A B}{A C} . \end{matrix}

Mint mondtuk, feladatunknak akkor és csak akkor létezik megoldása, ha

\begin{matrix} r^{'} + r^{''} ≧ O^{'} O^{''}, azaz \\ O^{'} C \cdot sin \frac{φ}{2} (1 + \frac{B C}{A C}) ≧ O^{'} C \cdot \frac{A B}{A C}, \end{matrix}

ahonnan rendezés után a

\begin{matrix} sin \frac{φ}{2} ≧ \frac{A B}{A C + B C} \end{matrix}

(1)

feltételt kapjuk.

2.a ábra

2.b ábra

Ha (1)-ben egyenlőség áll, akkor

k^{'}

és

k^{''}

érinti egymást, a feladatnak egy megoldása van, ha pedig a bal oldal nagyobb, akkor a körök metszik egymást, a megoldások száma kettő. A 2/b ábrán látható esetben, tehát ha a pontok egy egyenesen vannak és

C

nincs az

A B

intervallum belsejében ‐ egyébként nyilván nincs megoldás ‐ a két megoldás egybevágó.

II. megoldás. Legyen a szerkesztendő kör középpontja

O

, sugara

r

és használjuk a 3. ábra további jelöléseit is.

3. ábra

C O E

derékszögű háromszögben

\begin{matrix} sin \frac{φ}{2} = \frac{r}{C O} . \end{matrix}

Mivel

E O = A O = r,

ezért a szerkesztendő kör

O

középpontjára az

\begin{matrix} \frac{A O}{O C} = sin \frac{φ}{2} \end{matrix}

feltételt kapjuk.
Ismeretes, hogy azoknak a pontoknak a mértani helye a síkban, amelyeknek két adott ponttól ‐ az

A

és a

C

‐ mért távolságainak aránya adott, 1-től különböző pozitív szám ‐ most

0 < φ < 180^{\circ}, így 0 < sin \frac{φ}{2} < 1

‐ egy kör. (A bizonyítás megtalálható pl. Hajós György: Bevezetés a geometriába c. könyvének 124. oldalán). Az

O

pont tehát rajta van az

A

és a

C

pontokhoz tartozó

sin \frac{φ}{2}

aranyú ún. Apollóniusz-féle körön. És mivel

B O = r

és így

\begin{matrix} \frac{B O}{O C} = sin \frac{φ}{2} \end{matrix}

is igaz, az

O

ponton a

B

és

C

pontokhoz tartozó sin

\frac{φ}{2}

arányú Apollóniusz-kör is áthalad (hasonlóan az

A

és

B

pontok felező merőlegeséhez).

4. ábra

A három vonal ‐ két kör és egy egyenes ‐ közül kettőt megrajzolva megkapjuk a szerkesztendő kör középpontját, és egy pontja,

A

vagy

B

ismeretében magát a kört is (4. ábra). A feladatnak aszerint van 2, 1 vagy 0 megoldása, hogy a két kör metszi, érinti vagy pedig elkerüli egymást. Ebből némi számolással (1) adódik a megoldhatóság szükséges és elegendő feltételeként.