Kezdőlap


Feladat:	F.2661	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bíró 100 A. , Csáki Cs. , Fleiner T. , Hajnal Z. , Kecskés K. , Keleti T. , Kocsor A. , Nagy 124 G. , Paál Balázs , Pásztor G. , Siklér F. , Sustik M. , Tóth 178 G.
Füzet:	1988/április, 162 - 164. oldal		PDF \| MathML
Témakör(ök):	Függvények folytonossága, Háromszögek nevezetes tételei, Kombinatorikus geometria síkban, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1987/november: F.2661

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szabályos háromszög oldalát az első kérdés vizsgálatakor is választhatjuk egységnyinek. Legyenek tehát az egységnyi oldalú szabályos háromszög csúcsai $A_{1}, A_{2}, A_{3}$ , a velük szemben lévő oldalfelező pontok $B_{1}, B_{2}$ és $B_{3}$ . Ha adott a kerületen véges sok pont: $X_{1}, X_{2}, ..., X_{n}$ , akkor jelölje $F (Y)$ a háromszög egy tetszőleges $Y$ kerületi pontjának az ezen pontoktól való átlagtávolságát, azaz legyen

\begin{matrix} F (Y) = \frac{1}{n} \sum_{i = 1}^{n} d (Y, X_{i}), \end{matrix}

ahol

d (Y, X_{i})

Y

és az

X_{i}

pontok távolsága.

F (Y)

folytonos függvények összegének

n

-ed része, így maga is folytonos. Bizonyítanunk kellene tehát, hogy van olyan

t

érték, amelyre

Y

helyzetének a háromszög kerületén történő változtatásával

F (Y)

t

-nél nagyobb és a

t

-nél kisebb értéket is felvesz, ekkor ugyanis

F

folytonosságából következik, hogy van olyan

Y

pont is, melyre

F (Y) = t

1. ábra

Mindenekelőtt

t

értékét határozzuk meg, és egyben belátjuk, hogy ha létezik, akkor egyértelmű.
Ehhez két speciális esetet vizsgálunk,

n

értéke mindkét esetben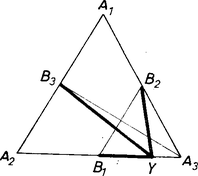

3

lesz:

I. A választott pontok a háromszög csúcsai, tehát

X_{1} = A_{1}, X_{2} = A_{2}, X_{3} = A_{3}

. Ekkor

F (Y) = 1 / 3 (d (Y, A_{1}) + d (Y, A_{2}) + d (Y, A_{3}))

. Ha

Y

A_{1} A_{2}

oldalon van (a háromszög szimmetriája alapján ezt az általánosság csorbítása nélkül föltehetjük), akkor

d (Y, A_{1}) + d (Y, A_{2}) = 1

és

Y

távolsága a harmadik csúcstól legalább akkora, mint a háromszög magassága (1. ábra), tehát

F (Y) \geq \frac{1}{3} (1 + \frac{\sqrt[]{3}}{2})

, és így

t

, ha létezik, nagyobb, vagy egyenlő, mint

\frac{1}{3} (1 + \frac{\sqrt[]{3}}{2})

2. ábra

II. A választott pontok ezután legyenek a háromszög oldalfelező pontjai:

X_{1} = B_{1}, X_{2} = B_{2}, X_{3} = B_{3}

. Most

F (Y) = 1 / 3 (d (Y, B_{1}) + d (Y, B_{2}) + d (Y, B_{3}))

. A szimmetria miatt feltehetjük, hogy

Y

B_{1} A_{3}

szakaszon van (2. ábra). A

B_{1} B_{2} A_{3}

szabályos háromszögben az oldal a legnagyobb távolság, így

d (Y, B_{1})

és

d (Y, B_{2})

akkor maximális, ha

Y

A_{3}

csúcsba esik. Az

Y B_{3} A_{3}

háromszögben pedig a tompaszöggel szemközti oldal ‐ az

A_{1} A_{2} A_{3}

háromszög

A_{3} B_{3}

magassága ‐ a legnagyobb. A három távolságra így a következő egyenlőtlenségeket írhatjuk fel:

\begin{matrix} d (Y, B_{1}) \leq 1 / 2, d (Y, B_{2}) \leq 1 / 2 és d (Y, B_{3}) \leq \sqrt[]{3} / 2, \end{matrix}

tehát ekkor

\begin{matrix} F (Y) \leq 1 / 3 (1 + \frac{\sqrt[]{3}}{2}) . \end{matrix}

A két esetet összevetve állíthatjuk, hogy ha

t

létezik, akkor értéke csak

1 / 3 (1 + \sqrt[]{3} / 2)

lehet. Belátjuk, hogy ez az érték rendelkezik az előírt tulajdonsággal.
Legyenek ehhez

X_{1}, X_{2}, ..., X_{n}

adott pontok a háromszög kerületén. Vizsgáljuk az

S = F (A_{1}) + F (A_{2}) + F (A_{3})

értéket. Ez nem más, mint a választott

X_{i}

pontoknak a háromszög csúcsaitól mért távolságátlagainak összege, azaz

\begin{matrix} S = \frac{1}{n} \sum_{i = 1}^{n} (d (X_{i}, A_{1}) + d (X_{i}, A_{2}) + d (X_{i}, A_{3})) . \end{matrix}

Mint láttuk,

d (X_{i}, A_{1}) + d (X_{i}, A_{2}) + d (X_{i}, A_{3}) \geq 3 t

, tehát ezen mennyiségek átlaga,

S \geq 3 t

, ami azt jelenti, hogy

F (A_{1}), F (A_{2})

és

F (A_{3})

közül egy legalább akkora, mint

t

.
Tekintsük ezután a

Q = F (B_{1}) + F (B_{2}) + F (B_{3})

összeget. Ez a választott

X_{i}

pontoknak a háromszög oldalfelező pontjaitól mért távolságátlagainak összege:

\begin{matrix} Q = \frac{1}{n} \sum_{i = 1}^{n} (d (X_{i}, B_{1}) + d (X_{i}, B_{2}) + d (X_{i}, B_{3})) . \end{matrix}

Mint a fentiekben bizonyítottuk,

d (X_{i}, B_{1}) + d (X_{i}, B_{2}) + d (X_{i}, B_{3}) \leq 3 t

, tehát

Q \leq 3 t

, ami azt jelenti, hogy

F (B_{1}), F (B_{2})

és

F (B_{3})

közül valamelyik legfeljebb akkora, mint

t

.
Találtunk tehát egy csúcsot, melyre az

F (Y)

függvény értéke

t

, vagy annál nagyobb, és egy oldalfelező pontot, melyre e függvényérték

t

, vagy annál kisebb. Ha valamelyik esetben egyenlőség van, akkor máris megfelelő pontot találtunk, egyébként pedig, mint azt a megoldás kezdetén megállapítottuk, az

F (Y)

függvény folytonosságából következik, hogy van legalább egy olyan

Y

pont a kerületen, melyre

F (Y) = t

Megjegyzések. 1. Mint azt többen észrevették, a feladat az F. 2641. feladat általánosítása. (Megoldás a lap 1987. évi 11. számának 380. oldalán.)

2. A vizsgált

F (Y)

függvények most a sík pontjain vannak értelmezve: a sík pontjaihoz rendelnek egy-egy számot. Ami az ilyen függvények folytonosságát illeti, ez ugyanúgy értelmezhető, mint a számhoz számot rendelő függvényeké, tehát egy

f : R \times R \to R

függvény akkor folytonos egy

X_{0}

pontban, ha minden

ε > 0

számhoz létezik olyan

δ > 0

szám, hogy a sík minden olyan

X

pontjára, amelyre

d (X, X_{0}) < δ

, fennáll, hogy

| f (X) - f (X_{0}) | < ε

.
Ismeretes, hogy ha egy

f

függvény a valós számokon van értelmezve és folytonos egy

I

intervallumban, akkor az

I

-beli számok képpontjainak

f (I)

-vel jelölt halmaza is intervallum, azaz

f

két tetszőleges

I

-beli értéke közé eső bármely értéket fölvesz az

I

intervallumban.
A feladatban ennek a tulajdonságnak egy ‐ nem a legáltalánosabb ‐ síkbeli változatát használjuk: a sík pontjaihoz számokat rendelő folytonos függvények egy

C

zárt görbén ‐ jelen esetben a szabályos háromszög kerületén ‐ fölvett értékei ugyancsak intervallumot alkotnak.