Kezdőlap


Feladat:	F.2653	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kincses Zoltán
Füzet:	1988/március, 107 - 109. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Trigonometriai azonosságok, Egyenlő szárú háromszögek geometriája, Háromszögek nevezetes tételei, Terület, felszín, Koszinusztétel alkalmazása, Szélsőérték-feladatok differenciálszámítás nélkül, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1987/október: F.2653

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B C$ háromszög területe $t$ , és hívjunk egy $e$ egyenest ‐ a háromszög $A$ csúcsára nézve ‐ jónak, ha a $B A C$ szögtartományból $t / 2$ területű háromszöget vág le. Nyilvánvaló, hogy minden területfelező egyenes jó a háromszög valamelyik csúcsára nézve (a súlyvonalak két csúcsra nézve is), ez azonban megfordítva nem igaz, hiszen egy jó egyenes nem feltétlenül belső pontban metszi az $A$ -ból induló oldalakat (1. ábra), és ilyenkor nem is felezi a háromszög területét.

1. ábra

Adott

f

területfelező egyenesre jelölje

d (f)

f

-nek a háromszög belsejébe eső szakaszát, ha pedig az

e

egyenes jó, akkor legyen

d^{*} (e)

e

megfelelő szögtartományba eső szakaszának a hossza. Ha

f

területfelező, akkor a fentiek szerint

d^{*} (f) = d (f) .

Módosítsuk feladatunkat, a területfelezők helyett vizsgáljuk a jó egyenesek bővebb halmazát, és keressük a

d^{*} (e)

mennyiségek minimumát. Mivel ez a számhalmaz bővebb, mint a feladatban szereplő

d (f)

mennyiségek halmaza, a minimumot szolgáltató

e_{0}

egyenesre

d^{*} (e_{0}) ≦ d (f)

minden

f

területfelező egyenes esetén. Ha ezután sikerül igazolnunk, hogy a talált jó

e_{0}

egyenes egyúttal területfelező is, akkor készen vagyunk,

e_{0}

lesz a keresett egyenes.
A

d^{*} (e)

mennyiségek minimumának meghatározásához először azt bizonyítjuk be, hogy egy konvex szögtartományból adott területű háromszöget levágó egyenesek közül annak a legkisebb a szögszárak közé eső szakasza, amelyik a szögtartományból egyenlő szárú háromszöget vág le. Legyen az

A

csúcsú konvex szögtartomány szöge

α,

A B C

háromszög az adott területű levágott háromszög (2. ábra), tegyük fel továbbá, hogy

A B < A C .

2. ábra

Ekkor az egyenlő szárú

A' B C

háromszög területe nagyobb, mint az

A B C

háromszög területe, hiszen

B C

oldaluk közös, a

B C

-hez tartozó magasság pedig az előbbi háromszögben nagyobb. Az

A' B C

háromszögből így a

B C

-vel párhuzamos egyenessel levághatunk egy

A' B' C'

háromszöget, amely egyenlő területű az

A B C

háromszöggel, és

B' C' < B C .

Ebből már következik a fenti állítás.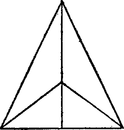

3. ábra

Ezután belátjuk, hogy két különböző szögű konvex szögtartományból adott területű egyenlő szárú háromszöget levágva, a nagyobb szög esetén lesz nagyobb a szögtartományt metsző egyenesnek a szárak közé eső szakasza. A 3. ábrán láthatjuk, hogy azonos hosszúságú szakaszok esetén a nagyobb szögtartományból levágott terület kisebb.
A fenti két észrevételből következik, hogy

d^{*} (e)

a háromszög legkisebb szögének felezőjére merőleges jó

e_{0}

egyenesre lesz minimális.
Meg kell még mutatnunk, hogy ez az

e_{0}

egyenes egyúttal a háromszög területét is felezi. Ehhez belátjuk, hogy az

A C

és az

A B

oldalakat egy-egy belső pontban metszi.
Az

α

a legkisebb szög, így a vele szemközti

a

oldalra

a ≦ b

és

a ≦ c .

Ha az

e_{0}

egyenes által levágott egyenlő szárú háromszög szára

h,

akkor azt kell igazolnunk, hogy

h ≦ b

és

h ≦ c .

Mivel az

e_{0}

jó, ezért

\begin{matrix} \frac{h^{2} \cdot sin α}{2} = \frac{t}{2} = \frac{b c \cdot sin α}{4}, ahonnan h = \sqrt[]{\frac{b c}{2}} . \end{matrix}

A háromszög-egyenlőtlenség következtében

c < a + b ≦ 2 b,

tehát

b \cdot c < 2 b^{2},

vagyis

\begin{matrix} \sqrt[]{\frac{b \cdot c}{2}} < b, és ugyanígy kapjuk, hogy \sqrt[]{\frac{b \cdot c}{2}} < c . \end{matrix}

II. megoldás. Használjuk a 4. ábra jelöléseit.Tegyük fel, hogy

B_{1} C_{1}

felezi a háromszög területét.

4. ábra

Ezért

\begin{matrix} \frac{b \cdot c \cdot sin α}{2} = x \cdot y \cdot sin α, amiből x \cdot y = \frac{b \cdot c}{2} . \end{matrix}

Számítsuk ki

B_{1} C_{1}

hosszát a koszinusz tétellel:

\begin{matrix} B_{1} C_{1}^{2} = x^{2} + y^{2} - 2 x y \cdot cos α = {(x - y)}^{2} + 2 x y (1 - cos α), \end{matrix}

amiből

x \cdot y

fenti alakjával

\begin{matrix} B_{1} C_{1}^{2} = {(x - y)}^{2} + b c (1 - cos α) . \end{matrix}

Ebből látható, hogy

B_{1} C_{1}

akkor a legkisebb, ha

\begin{matrix} x = y, \end{matrix}

azaz a lemetszett háromszög egyenlő szárú, a szárak hossza pedig

\begin{matrix} x = y = \sqrt[]{\frac{b \cdot c}{2}} . \end{matrix}

A levágott egyenlő szárú háromszög alapja ekkor

\begin{matrix} B_{1} C_{1} = \sqrt[]{b c (1 - cos α)} . \end{matrix}

Alakítsuk ezt át, fölhasználva a

b c \cdot sin α = 2 t

összefüggést :

\begin{matrix} B_{1} C_{1} = \sqrt[]{2 t \frac{1 - cos α}{sin α}}, \end{matrix}

ahol

t

A B C

háromszög területe. Ezután az

1 - cos α = 2 \cdot sin^{2} \frac{α}{2}

és a

sin α = 2 sin \frac{α}{2} \cdot cos \frac{α}{2}

azonosságok alapján

\begin{matrix} B_{1} C_{1} = \sqrt[]{2 t \cdot tg \frac{α}{2}}, \end{matrix}

ami azt jelenti, hogy

B_{1} C_{1}

a háromszög szögeitől függően akkor a legkisebb, ha az

α

szög a legkisebb, hiszen a tangens függvény monoton növekvő a

(0, π / 2)

intervallumban.
Az első megoldásban látottakhoz hasonlóan most is meg kell mutatnunk, hogy ha

α

a legkisebb szög, akkor

B_{1}

és

C_{1}

A C,

illetve

A B

oldal belső pontja.

Megjegyzések: 1. A fenti megoldásokban talált szakasz nem a legrövidebb a háromszög területét felező ,,vonalak'' közül.

5. ábra

Tegyük fel, hogy az 5. ábra

B_{1} C_{1}

szakasza a legrövidebb területfelező szakasz, és legyen a szögfelezőjének a

B_{1} C_{1}

-gyel való metszéspontja

M_{1} .

A M_{1} C_{1}

háromszög nem egyenlő szárú, ezért az eddigiek alapján van olyan

C_{2} M_{2}

szakasz, amely rövidebb

C_{1} M_{1}

-nél, és ugyanakkora területű háromszöget metsz le az

\frac{α}{2}

szögű szögtartományból, mint

C_{1} M_{1} .

A szögfelezőre vonatkozó tengelyes szimmetria miatt ekkor hasonló igaz a

B_{2} M_{2}

szakaszra is. Ez azt jelenti, hogy a

C_{2} M_{2} B_{2}

töröttvonal is felezi a háromszög területét, hossza pedig rövidebb

B_{1} C_{1}

-nél. Az eljárást folytatva egyre rövidebb területfelező ,,vonalhoz'' jutunk. Bebizonyítható, hogy a legrövidebb felezővonal egy körív.

2. Az első megoldás bizonyos értelemben hiányos. Az abban vizsgált területeket, illetve egy adott szög szárait metsző jó egyenesekre a

d^{*} (e)

mennyiséget magától értetődően folytonosnak tekintettük, és azt is természetesnek vettük, hogy a keresett minimum létezik. A II. megoldásban a

B_{1} C_{1}

szakasz analitikus alakja mutatja, hogy ez a függvény valóban folytonos.

3. A legkisebb területfelező szakasz könnyen megszerkeszthető. Szerkeszthető ugyanis az

x = y = \sqrt[]{\frac{b \cdot c}{2}}

mint

b

és

\frac{c}{2}

mértani közepe.