Feladat: F.2649 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Balogh 171 J. ,  Benczúr P. ,  Binder Zsuzsanna ,  Bíró 700 A. ,  Csanádi P. ,  Csirik J. ,  Fleiner T. ,  Gutai Zs. ,  Hajnal Z. ,  Hídvégi Z. ,  Illés T. ,  Kecskés K. ,  Keleti T. ,  Makay L. ,  Pásztor G. ,  Peták A. ,  Siklér F. ,  Takách G. ,  Tavaszi G. ,  Tóth 178 G. 
Füzet: 1988/február, 65 - 67. oldal  PDF  |  MathML 
Témakör(ök): Harmadfokú (és arra visszavezethető) egyenletek, Geometriai egyenlőtlenségek, Függvények folytonossága, Ceva-tétel, Háromszögek nevezetes tételei, Konstruktív megoldási módszer, Feladat
Hivatkozás(ok):Feladatok: 1987/szeptember: F.2649

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a feladat kérdésére igenlő a válasz, ilyen ponthármas minden háromszöghöz létezik. Vegyünk föl egy tetszőleges háromszöget, és válasszuk meg a betűzést úgy, hogy az A, B, C csúcsokkal szemközti a, b, c oldalakra a≤b≤c teljesüljön. Jelöljük a háromszög kerületének harmadát h-val. Ekkor nyilván 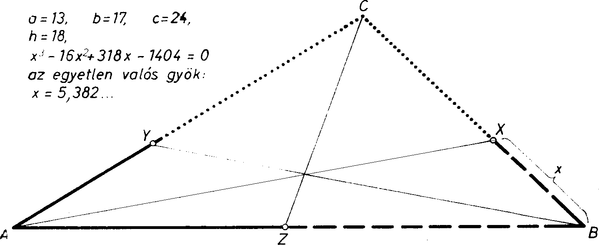a≤h≤c.

 
 

Ha X, Y és Z tetszőleges belső pontok a BC, CA, illetve AB oldalakon, akkor a b) feltétel pontosan akkor teljesül, ha
XC+CY=YA+AZ=ZB+BX=h.(1)

Ha a BX távolságot x-szel jelöljük, akkor X pontosan akkor belső pontja a BC oldalnak, ha
0<x<a,(2)
másfelől (1) alapján a, c, h és x segítségével valamennyi további szóban forgó távolság kifejezhető:
XC=a-x,CY=h-XC=h-a+x,ZB=h-BX=h-x,AZ=c-ZB=c-h+x,  végül  AY=h-AZ=2h-c-x.

Vegyük most szemügyre az a) feltételt. Ez pontosan akkor teljesül, ha (2) mellett fennállnak még a
0<ZB=h-x<c  és a  (3)0<CY=h-a+x<begyenlőtlenségek.(4)

Mivel 0<x<a≤h≤c, ezért (3) teljesül, és a (4)-beli CY is pozitív. A (2) mellett tehát a
h-a+x<b(4')
feltételnek kell még teljesülnie, ami x-re nézve együttesen a
0<x<min(a,a+b-h)(5)
egyenlőtlenséget jelenti.
Ami a c) feltételt illeti, ez Ceva tételének megfordítása szerint pontosan akkor teljesül, ha
AZ⋅BX⋅CY=ZB⋅XC⋅YA,
vagyis
(c-h+x)x(h-a+x)=(h-x)(a-x)(2h-c-x).(6)

Jelölje p(x) és q(x) a (6) bal, illetve jobb oldalán álló harmadfokú polinomot. Állításunk bizonyításához azt kell megmutatnunk, hogy létezik olyan x0, melyre teljesül (5), másfelől p(x0)=q(x0). Tekintsük a p(x) és q(x) polinomokat a 0, a és az a+b-h helyeken.
 
p(0)=0, hisz a második tényező 0;
q(0)=h⋅a⋅(2h-c)>0,
 

hisz 2h-c=2a+2b-c3, ami a háromszög-egyenlőtlenség szerint valóban pozitív.
p(a)=(a+c-h)a⋅h>0, hisz c≥h és a>0, és
q(a)=0, hisz a második tényező 0.
Végül
p(a+b-h)=(a+b+c-2h)(a+b-h)b=h(a+b-h)⋅b>0,
hisz a háromszög-egyenlőtlenség szerint a+b>c≥h és q(a+b-h)=0, hisz a harmadik tényező 0.
Összefoglalva azt kaptuk, hogy
p(0)<q(0),p(a)>q(a)ésp(a+b-h)>q(a+b-h).

Minthogy p is és q is folytonos függvénye x-nek, az első két egyenlőtlenségből következik, hogy van olyan pozitív, a-nál kisebb x'0, amelyre p(x0')=q(x0'), az első és a harmadik egyenlőtlenségből pedig, hogy van olyan pozitív, (a+b-h)-nál kisebb x''0, amelyre p(x0'')=q(x0''). Mindenképpen van tehát olyan pozitív, (5)-nek eleget tevő x0, amelyre p(x0)=q(x0). Ha most tekintjük a BC szakasz azon belső X pontját, amelyre BX=x0, a CA szakasz azon Y pontját, amelyre CY=h-a+x0 és az AB szakasz azon Z pontját, amelyre ZB=h-x0, akkor (5) szerint Y és Z is belső pontok, X, Y és Z választása miatt teljesül rájuk a b) feltétel, végül x0 választása és a Ceva-tétel megfordítása szerint az AX, BY és CZ egyenesek valóban egy ponton mennek át.
Ezzel beláttuk, hogy minden ABC háromszöghöz található megfelelő X, Y, Z ponthármas.
 
Megjegyzések: 1. Könnyű belátni, hogy minden háromszöghöz pontosan egy megfelelő ponthármas létezik.
2. Sok olyan dolgozat érkezett, amelyben a megoldó felírta a (6) egyenletet, belátta, hogy annak van megoldása, de nem foglalkozott azzal a kérdéssel, hogy a kapott megoldáshoz tartozó X, Y, Z pontok valóban belső pontjai-e a háromszög megfelelő oldalainak. Az ilyen megoldások nem kaptak maximális pontszámot.