Feladat: F.2642 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Baboss Csaba ,  Bánkövi Johanna ,  Beke T. ,  Benczúr A. ,  Bereczky Á. ,  Binder Zsuzsanna ,  Bukszár J. ,  Csöry S. ,  Cynolter G. ,  Dienes J. ,  Gács A. ,  Hadnagy Éva ,  Hajdú G. ,  Károlyi Gy. ,  Keleti Tamás ,  Kincses Z. ,  Majoros L. ,  Máté Nóra ,  Rimányi R. ,  Sustik M. ,  Szabó 484 P. ,  Szabó 668 T. ,  Szalay Gy. ,  Talata I. ,  Tavaszi G. ,  Veres E. ,  Wiandt T. ,  Wolkensdorfer P. ,  Zaránd G. ,  Zsigmond L. 
Füzet: 1988/március, 99 - 102. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Súlypont, Hossz, kerület, Terület, felszín, Paralelogrammák, Téglalapok, Feladat
Hivatkozás(ok):Feladatok: 1987/május: F.2642

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vizsgáljuk először, hogy adott ABC háromszögre mi azon P pontok TB halmaza a síkban, amelyekre a szóban forgó háromszögek közül kettő, például a PAB és a PBC háromszögek területe egyenlő. Ha P≡B, akkor a háromszögek szakasszá fajulnak, területük nulla, így B∈TB. Egyébként e két háromszög PB oldala közös, így P≢B akkor és csak akkor eleme TB-nek, ha az A és a C csúcsok egyenlő távol vannak a PB egyenestől.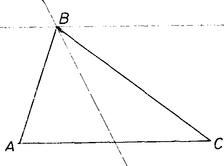

 
 
1. ábra
 

Ha a PB egyenes elválasztja A-t és C-t, akkor a fentiek szerint át kell haladjon az AC felezőpontján, ha pedig nem, akkor nyilván párhuzamos AC-vel. Ennek a metsző egyenespárnak pedig nyilván minden pontja hozzátartozik a TB halmazhoz (1. ábra).
Ha most mindhárom háromszög egyenlő területű, akkor P bármely két ilyen egyenespárnak pontja. Tetszőleges ABC háromszöghöz négy ilyen pont van (2. ábra), a háromszög súlypontja, illetve a csúcsok tükörképe a szemközti oldal felezőpontjára.
 
 
2. ábra
 

Vizsgáljuk most meg, hogy erre a négy pontra milyen háromszögekben teljesül a feladat második, a kerületekről szóló föltétele. Tekintsük először az ABC háromszög S súlypontját. Ha például az SAB és az SBC háromszögek kerülete egyenlő, akkor
SA+BA=SC+BC.(1)
Azt állítjuk, hogy (1) pontosan akkor teljesül, ha az ABC háromszög egyenlő szárú, mégpedig úgy, hogy a B csúcsból induló oldalak egyenlők.
Ha BA=BC, akkor (1) nyilván igaz, hiszen a B-ből induló súlyvonal egyúttal az AC felező merőlegese is. Ha pedig például BA>BC, akkor a B-ből induló súlyvonal teljes egészében ‐ a másik végpontja kivételével ‐ az AC felező merőlegesének a C-t tartalmazó oldalán halad. Ekkor pedig SA>SC, hisz S, a súlypont, belső pontja a súlyvonalnak (3. ábra). A két egyenlőtlenséget összeadva SA+BA>SC+BC, vagyis (1) nem állhat fenn.
 
 
3. ábra
 

Egy ABC háromszög S súlypontjára tehát akkor és csak akkor lesz egyenlő az SAB, SBC és az SCA háromszögek kerülete, ha az ABC bármely két oldala egyenlő, azaz a háromszög szabályos.
Tekintsük most a P további három lehetséges helyzete közül például a PA pontot, az A-nak a BC felezőpontjára vonatkozó tükörképét. Az ACPAB négyszög paralelogramma, így az APAB és az APAC háromszögek kerülete egyenlő. A harmadik, PABC háromszög pedig éppen akkor lesz ezekkel egyenlő kerületű, ha az előbbi paralelogramma átlói egyenlők, maga a paralelogramma pedig így téglalap. Ez pedig pontosan akkor teljesül, ha az ABC háromszögben az A csúcsnál derékszög van.
Azt kaptuk, hogy a megadott tulajdonságú P pont akkor és csak akkor létezik, ha az ABC háromszög szabályos, vagy pedig derékszögű. Előbbi esetben P a háromszög súlypontja, az utóbbiban pedig a derékszögű csúcs tükörképe az átfogó felezőpontjára.
 

Megjegyzés. A PAB és a PBC háromszögek kerülete pontosan akkor egyenlő, ha PA+AB=PC+CB, azaz PA-PC=CB-AB. Az ilyen tulajdonságú P pontok AB=BC esetén az AC felező merőlegesén, egyébként pedig egy hiperbola egyik ágán helyezkednek el (4. ábra). A hiperbola fókuszai A és C, a hiperbolaág pedig áthalad a B-nek az AC felező merőlegesére vonatkozó tükörképén.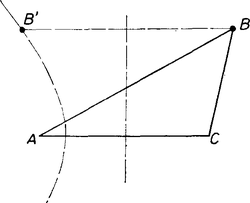
 
 
4. ábra
 

II. megoldás. Jelöljük a PA, PB, PC szakaszok hosszát rendre x,y,z-vel, és legyen a PAB, PBC és PCA háromszögek kerülete 2s. Ekkor
2s=x+y+c=x+z+b=y+z+a.
Mindegyik egyenlet mindkét oldalából x+y+z-t kivonva kapjuk, hogy
c-z=b-y=a-x.(2)

Mivel a területek is megegyeznek, a Heron képlet szerint :
s(s-x)(s-y)(s-c)=s(s-x)(s-z)(s-b)=s(s-y)(s-z)(s-a).
Négyzetre emelve és s(s-x)(s-y)(s-z)-vel osztva, ami nem 0,
s-cs-z=s-bs-y=s-as-x  adódik.(3)
Vegyük figyelembe, hogy pl.
s-cs-z=s-z+z-cs-z=1+z-cs-z,
és így (3) a következőképpen írható:
1-c-zs-z=1-b-ys-y=1-a-xs-x.(4)
(2) szerint e törtek számlálói egyenlők, így (4) csak úgy teljesülhet, ha a nevezők is azok, vagy ha a számlálók értéke nulla. Ha tehát az ABC háromszögre és a P pontra teljesül a feladat feltétele, akkor a bevezetett jelölésekkel vagy


a)s-z=s-y=s-x,vagy pedigb)c-z=b-y=a-x=0.

Az a) esetben x=y=z, de akkor (2) szerint a=b=c, tehát a háromszög szabályos.
A b) esetben a=x, b=y és c=z, azaz AB=PC, BC=PA és CA=PB. Bárhogy is választunk ki tehát a négy pont, A,B,C és P közül kettőt-kettőt, a párokat összekötő szakaszok egyenlők. E négy pont tehát ‐ valamilyen sorrendben ‐ egy olyan paralelogramma négy csúcsa, amelynek egyenlő hosszúak az átlói, a négyszög ezért téglalap, az ABC háromszög pedig derékszögű.
Könnyen látható, hogy a talált esetekben létezik a feladat feltételeinek eleget tevő P pont. Az a) esetben P-nek a csúcsoktól mért távolságai egyenlők, így P az oldalfelező merőlegesek metszéspontja (azaz egyben a háromszög súlypontja is). A b) esetben pedig P az ABC derékszögű háromszög téglalappá történő kiegészítése után adódó negyedik csúcs.