Kezdőlap


Feladat:	F.2636	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bánkövi Johanna , Beke T. , Benczúr A. , Bereczky Á. , Csűrös M. , Domokos P. , Eckert B. , Farnadi Á. , Fazekas Zs. , Gács A. , Hadnagy Éva , Hahn Zsuzsa , Hajnal Z. , Illés T. , Jalsovszky P. , Kelemen Eszter , Keleti T. , Kiss 303 B. , Kovács 475 P. , Kovács 969 T. , Kovács Á. , Lovro Adrienn , Márton Zs. , Máté Nóra , Mikusi Cs. , Németh L. , Németh V. , Pongor G. , Rimányi R. , Schmidt E. , Szabó 668 T. , Szabó Péter , Szalay Gy. , Szepesi Zsuzsanna , Talata I. , Tornyi L. , Tóth 178 G. , Varga Zs. , Vörös P. , Zsigmond L.
Füzet:	1987/november, 376 - 378. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Terület, felszín, Trapézok, Húrnégyszögek, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1987/április: F.2636

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a szabályos háromszög oldalát $a$ -val, az $X A B$ szöget pedig $α$ -val (1. ábr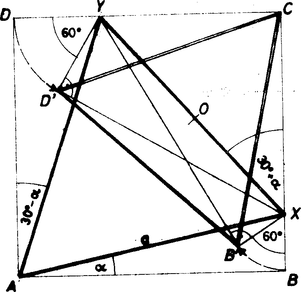a).

1. ábra

Ekkor

Y A D ∢ = 30^{\circ} - α

és

Y X C ∢ = 30^{\circ} + α

. Az ábra derékszögű háromszögeiből:

\begin{matrix} A B = a \cdot cos α, A D = a \cdot cos (30^{\circ} - α) \\ és X C = a \cdot cos (30^{\circ} + α) . \end{matrix}

A téglalapból megmaradó három derékszögű háromszög területe így

\begin{matrix} t_{A B X} & = \frac{1}{2} \cdot a^{2} \cdot cos α \cdot sin α, \\ t_{A D Y} & = \frac{1}{2} \cdot a^{2} \cdot cos (30^{\circ} - α) \cdot sin (30^{\circ} - α), \\ t_{X C Y} & = \frac{1}{2} \cdot a^{2} \cdot cos (30^{\circ} + α) \cdot sin (30^{\circ} + α) . \end{matrix}

Bebizonyítjuk, hogy az első két terület összege ugyanannyi, mint a harmadik.

\begin{matrix} t_{A B X} + t_{A D Y} = \frac{1}{2} \cdot a^{2} \cdot cos α \cdot sin α + \frac{1}{2} \cdot a^{2} \cdot cos (30^{\circ} - α) \cdot sin (30^{\circ} - α) = \\ = \frac{1}{4} \cdot a^{2} [sin 2 α + sin (60^{\circ} - 2 α)] = \frac{1}{4} \cdot a^{2} \cdot 2 \cdot sin 30^{\circ} \cdot cos (30^{\circ} - 2 α), \end{matrix}

ahol az utolsó lépésben fölhasználtuk a

sin x + sin y = 2 \cdot sin \frac{x + y}{2} \cdot cos \frac{x - y}{2}

azonosságot. Figyelembe véve, hogy

cos (30^{\circ} - 2 α) = sin (60^{\circ} + 2 α)

, a területek összegére kapott előbbi kifejezésünk így alakul:

\begin{matrix} t_{A B X} + t_{A D Y} = \frac{1}{4} \cdot a^{2} \cdot sin (60^{\circ} + 2 α) = \frac{1}{2} \cdot a^{2} \cdot sin (30^{\circ} + α) \cdot cos (30^{\circ} + α), \end{matrix}

ami valóban az

X C Y

háromszög területe. Ezzel a feladat állítását bebizonyítottuk.

II. megoldás. Ismét azt mutatjuk meg, hogy az

X C Y

háromszög területe egyenlő az

A B X

és

A D Y

háromszögek területének összegével. E derékszögű háromszögek átfogója egyenlő, ezért elegendő belátni, hogy az utóbbi két háromszögben az átfogóhoz tartozó magasságok összege az

X C Y

háromszög átfogóhoz tartozó magasságával egyenlő.
Forgassuk el az

A D Y

háromszöget az

Y

, az

A B X

háromszöget pedig az

X

csúcsa körül

60^{\circ}

-kal úgy, hogy az előbbi háromszög

A Y

, az utóbbinak pedig az

A X

oldala menjen át az

X Y

oldalba. Az egyes elforgatások után a

D

és a

B

képe legyen

D'

illetve

B'

(1. ábra).
Az elforgatott háromszögek derékszögű csúcsa, a

D'

és a

B'

rajta van az

X Y

szakasz Thalész-körén, csakúgy mint a

C

csúcs, ezért a

C D' B'

háromszög körülírt körének középpontja az

X Y

szakasz

O

felezőpontja. Megmutatjuk, hogy

O

ennek a háromszögnek súlypontja is, vagyis a háromszög szabályos.
A

60^{\circ}

-os elforgatás miatt

D' Y C ∢ = 120^{\circ}

, a

C Y D' B'

húrnégyszögben tehát

C B' D' ∢ = 60^{\circ}

valóban, és hasonlóan kapjuk, hogy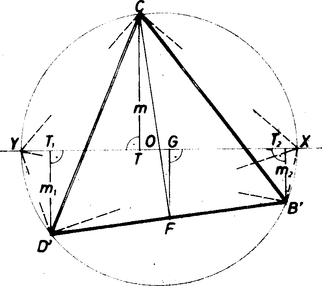

C D' B' ∢ = 60^{\circ}

2. ábra

Tekintsük ezután a

C D' B'

háromszöget a súlypontján áthaladó

X Y

egyenessel, és használjuk a 2. ábra jelöléseit. Ezen az ábrán

m_{1}

X Y D'

háromszög átfogóhoz tartozó magassága,

m_{2}

és

m

pedig ugyanilyen magasság az

X Y B'

, illetve az

X Y C

háromszögben. A bevezetőben mondottak szerint azt kell megmutatnunk, hogy

\begin{matrix} m = m_{1} + m_{2} . \end{matrix}

(1)

Az ábráról leolvasható, hogy a

B' T_{2} T_{1} D'

trapéz középvonala,

\begin{matrix} F G = \frac{m_{1} + m}{2} . \end{matrix}

(2)

F G O \sim C T O

hasonlóságból:

\begin{matrix} m : F G = O C : F O, \end{matrix}

s mivel a jobb oldal 2 ‐ hiszen

O

súlypont ‐

\begin{matrix} m = 2 F G . \end{matrix}

(3)

(2) és (3)-ból következik (1), amit bizonyítani akartunk.

Megjegyzés. Fölmerülhet a kérdés, vajon mely téglalapokból vágható ki a feladat követelményei szerinti szabályos háromszög. Világos, hogy

α

-ra

0 ≦ α ≦ 30^{\circ}

, azaz

0 ≦ tg α ≦ \frac{1}{\sqrt[]{3}}

. A téglalap oldalainak aránya

\begin{matrix} \frac{A D}{A B} = \frac{a \cdot cos (30^{\circ} - α)}{a \cdot cos α} = \frac{\sqrt[]{3}}{2} + \frac{1}{2} \cdot tg α, \end{matrix}

vagyis a

\begin{matrix} \frac{\sqrt[]{3}}{2} ≦ \frac{A D}{A B} ≦ \frac{\sqrt[]{3}}{2} + \frac{1}{2} \sqrt[]{3} = \frac{2}{\sqrt[]{3}} \end{matrix}

egyenlőtlenségnek kell teljesülnie.