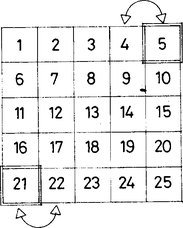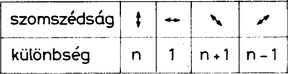|
| Feladat: |
F.2633 |
Korcsoport: 16-17 |
Nehézségi fok: nehéz |
| Megoldó(k): |
Benczúr A. , Bereczky Á. , Binder Zsuzsanna , Cynolter G. , Hajdú G. , Hajnal Z. , Keleti T. , Majoros L. , Rimányi R. , Szabó 484 P. , Szalay Gy. , Veres E. |
| Füzet: |
1987/december,
440 - 442. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Számelrendezések, Kombinatorikus geometria síkban, Kombinatorikai leszámolási problémák, Teljes indukció módszere, Feladat |
| Hivatkozás(ok): | Feladatok: 1987/április: F.2633 |
|
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ha akkor a táblázat csak egyféleképpen tölthető ki, ha pedig akkor nyilván bármely kitöltés megfelelő. Ez 4! = 24 lehetőséget jelent, ha a forgatással és tükrözéssel egymásba vihető kitöltéseket megkülönböztetjük egymástól, egyébként pedig -at. A továbbiakban az esettel foglalkozunk.
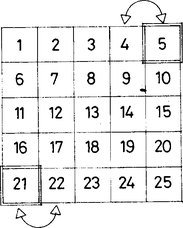 1.a ábra
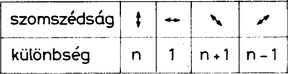 1.b ábra
Az 1/a ábrán az esetre bemutatott kitöltés nyilván megfelelő. Az 1/b ábrán a különbségek láthatók a négyféle lehetséges szomszédságra. A bal alsó és a jobb fölső sarokmezőnek nincs főátló irányú szomszédja, így az itteni számok kicserélhetők a mellettük állókkal. Azt állítjuk, hogy nincsen az így kapható összesen négy megfelelő kitöltéstől lényegesen különböző, azaz tükrözéssel és forgatással minden megoldás a fenti négy valamelyikébe vihető.
Tekintsünk egy megfelelő kitöltést, és legyen . Ha jelöli az és az y mezők között a szomszédos mezőkön át vezető legrövidebb út hosszát (tehát ahogyan egy király mozog a sakktáblán), akkor nyilván 1≦d(x,y)≦n-1, másrészt a kitöltésből adódik, hogy Ha két mezőre (1)-ben egyenlőség van, akkor a legrövidebb úton x ből y-ig haladva (x<y föltehető) minden lépésben legalább D-t kell haladnunk. Mivel a feltétel szerint ennél többet egyszer sem haladhatunk, így az útbaejtett mezők egyértelműen meghatározottak: x, x+D, x+2D, ..., x+d(x,y)⋅D=y. Ilyenkor tehát pontosan egy d(x,y) hosszúságú út vezet x és y között, és így a két mező vagy szomszédos (ha d(x,y)=1), vagy pedig egy d(x,y)+1 hosszúságú átló két szélső mezeje, ahol átlónak a 2. ábrán látható mezők sorozatát nevezzük. Hivjuk a kitöltésnek ezt a tulajdonságát "merev átló'' tulajdonságnak.
 2. ábra
E tulajdonság szerint 1 és n2 egy n hosszúságú átló két szélső mezeje. Ilyen átló kettő van, és föltehető, hogy az 1 a bal fölső, az n2 pedig a jobb alsó sarokmező. A táblázat leghosszabb főátlója tehát az 1 ábra szerint van kitöltve, az i-edik sor i-edik mezőjében 1+(i-1)D=ai áll.
Ekkor | d(n2-1,1)≧n2-2n+1>n-2,azazd(n2-1,1)=n-1, |
így n2-1 az utolsó sorban, vagy pedig az utolsó oszlopban van. Föltehető, hogy az első eset valósul meg, azaz n2-1 az utolsó sorban van.
Most az i-re vonatkozó teljes indukcióval belátjuk, hogy
A) ha (i-1)n+1≦x≦i⋅n, akkor x az i -edik sorban van és aszerint áll az átlóselem, ai előtt vagy pedig utána, hogy kisebb, vagy nagyobb ai -nél, úgy, ahogyan ez az 1 ábra kitöltésében látható.
i=1 -re ez azt jelenti, hogy ha x≦n , akkor x az első sorban van. Mivel | d(n2-1,x)≧n2-1-xn+1≧n2-n-1n+1>n-2, |
ezért d(n2-1,x)=n-1, és ugyanígy kapjuk, hogy d(n2,x)=n-1. A legalsó sor két különböző mezőjéről tehát nem vezet (n-1)-nél rövidebb út az x -hez, így az valóban az első sorban van.
Legyen most 1<i≦n és tegyük fel, hogy az i -nél kisebb sorszámú sorokra az állítás igaz. Így persze az i -edik sorban minden elem legalább (i-1)n+1. Mivel az (i-1) -edik sor maximális eleme (i-1)n és az i -edik sor bármely elemének legalább két fölső szomszédja van, az i -edik sorban valóban nem állhat (i-1)n-1+D=i⋅n-nél nagyobb szám. Ugyanígy kapjuk, hogy az i -edik sorban az i-nél kisebb sorszámú helyeken minden szám legfeljebb ai-1-1+D<ai. Ezzel az A) állítást igazoltuk.
Hívjuk most i -edik átlónak az első sor i -edik mezőjén kezdődő főátlót. Az i -re vonatkozó teljes indukcióval igazoljuk, hogy
B) ha 1≦i≦n-2, akkor az i -edik átlóban az i, i+D, i+2D, ..., i+(n-i)D számok állnak az 1 ábra kitöltésének megfelelően.
Ha i=1, akkor éppen a leghosszabb főátlóról van szó, így az állítás igaz. Legyen most 1<i≦n-2.
Az indukciós föltevés miatt így egyrészt az első sorban i csak a 3/a ábra satírozott részén lehet, másrészt az (n-i+1) -edik sorban az átlóselem, an-i+1 után már csak a legutolsó mező maradt kitöltetlen (3/b ábra). A sor maximális eleme, Mi=(n-i+1)n tehát csak ide kerülhet.
 3.a ábra
 3.b ábra
Így a jobb fölső sarokban lévő (n-i+1) oldalú négyzet két szemközti sorában lévén d(i,Mi)=n-i, ezért (1)-ben most egyenlőség van, hisz Mi-iD=n-i. Mivel pedig n-i>1, ezért a merev átló tulajdonság szerint az állítás i-re is teljesül. Ezzel a B) állítást is bebizonyítottuk.
Végül ha i=n-1, akkor annyi most is igaz, hogy a második sorban a maximális elem, M2=2n az utolsó mezőben áll. Ekkor viszont d(n-1,2n)=1, így csak annyit állíthatunk, hogy az n-1 és a 2n mezők szomszédosak, így az első sor-ban n-1 az utolsó előtti, vagy pedig az utolsó mező.
A legalsó sor mezőin kezdődő főátlók felhasználásával hasonlóan bizonyítható, hogy a leghosszabb főátló alatti átlók kitöltése is csak az 1 ábra szerint alakulhat (itt is lehetséges persze az utolsó sor első két elemének a cseréje). Ezzel bizonyításunk teljes, a feladatnak valóban csak az adott típusú megoldása létezik.
Tükrözéssel és forgatással mind a négy megoldásból 8‐8 készíthető, így ha ezeket is megkülönböztetjük, akkor az n>2 esetben 32-féle megfelelő kitöltése létezik a táblázatnak.
|
|
 PDF |
PDF |  MathML
MathML