| Feladat: | F.2625 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Beke T. , Benczúr A. , Bereczky Á. , Cynolter G. , Eckert B. , Hajdú G. , Kovács 969 T. , Leier Z. , Lozsi I. , Majoros L. , Rimányi R. , Szalay Gy. , Tasi Andrea , Tasnádi T. , Wiandt T. | ||
| Füzet: | 1987/október, 302 - 303. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai bizonyítások, Terület, felszín, Egyéb sokszögek geometriája, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1987/február: F.2625 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Tegyük fel, hogy az , , , egyenesek mindegyike keresztülmegy -n és felezi az területét. Tegyük fel azt is, hogy -et körül pozitív irányba forgatva először -t, azután -at stb., végül -et kapjuk. Minthogy konvex, pedig belső pont, kerületét minden egyenes pontosan kétszer metszi, az darab egyenes tehát -et darab konvex sokszögre bontja. Legyenek ezek ‐ pozitív körüljárás szerint ‐ rendre , , , , , A és az éppen "szemben'' vannak egymással, s mindkettőt és határolja. és területe nyilván egyenlő, hiszen és is felezi területét. Tükrözzük -t -re, a kapott sokszög legyen . -t és -t most -nek és -nek azonos, -ből induló félegyenesei határolják (vagyis azonos, által határolt szögtartományba esnek). és területe egyenlő, tehát nem eshet teljes egészében belsejébe, de nem is foglalhatja egészen magában -t. -nek és -nek van tehát közös pontja kerületén. Ugyanez igaz és -re, ahol az -nek -re vonatkozó tükörképe. 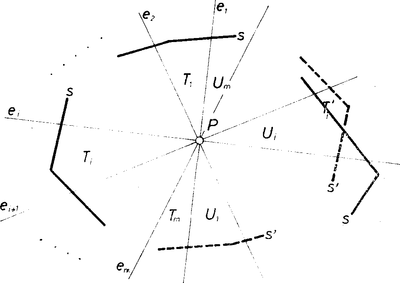 Ha most -et tükrözzük -re, akkor a kapott tükörkép a , , , , , , , sokszögek mindegyikét metszeni fogja kerületének egy-egy (semelyik -hez nem tartozó) pontjában. -et tehát legalább különböző pontban metszi. -nek és -nek nincs közös oldalegyenese, különben -nek volnának párhuzamos oldalai. Így minden oldalegyenese legfeljebb két pontban metszi -et. mert konvex. -nek oldalegyenese van, tehát és metszéspontjainak a száma legföljebb A metszéspontok számát -val jelölve azt kapjuk tehát, hogy ahonnan következik. Ezzel beláttuk, hogy a -n átmenő területfelező egyenesek száma valóban legföljebb Ez a szám el is érhető, mint azt a páratlan oldalú szabályos sokszögek mutatják ( a középpont). Ha egy téglalap két szemközti oldalához két egyenlő területű sokszöget illesztünk úgy, hogy a kapott sokszög konvex maradjon, akkor az így kapott sokszögnek végtelen sok, a téglalap középpontján áthaladó területfelező egyenese van. Ez mutatja, hogy nem hagyható el a feladatnak az a kikötése, hogy -nek ne legyenek párhuzamos oldalai. Ha nem konvex, akkor pedig már az is nehezen megválaszolható kérdés, hogy mikor nevezzünk egy egyenest területfelezőnek. |