Kezdőlap


Feladat:	F.2613	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Tasi Andrea
Füzet:	1987/május, 207 - 209. oldal		PDF \| MathML
Témakör(ök):	Racionális számok és tulajdonságaik, Indirekt bizonyítási mód, Szabályos testek, Koszinusztétel alkalmazása, Helyvektorok, Feladat
Hivatkozás(ok):	Feladatok: 1986/december: F.2613

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kocka esetére a válasz nyilvánvalóan igenlő. Az adott koordináta-rendszer hosszegységével egyenlő élű kocka beállítható a rendszerbe úgy, hogy minden csúcsának koordinátái a $0$ és $1$ számok ismétléses variációi ( $8$ csúcs, $8$ variáció):

\begin{matrix} (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1) . \end{matrix}

(1)

A szokásos kifejezéssel élve: mind a

8

csúcs rácspont, ez a kocka rácskocka.
Egy másik igen egyszerű megoldás: minden csúcs mindhárom koordinátája abszolút értékben

1,

és eléjük írjuk a "

+

" és "

-

" előjelek minden lehetséges ismétléses variációját :

\begin{matrix} (+ 1, + 1, + 1), (+ 1, + 1, - 1), (+ 1, - 1, + 1), (+ 1, - 1, - 1), (- 1, + 1, + 1), \\ (- 1, + 1, - 1), (- 1, - 1, + 1), (- 1, - 1, - 1) . & (2) \end{matrix}

Szabályos tetraéder csúcsait úgy kapjuk, ha kiválasztjuk a kocka egy csúcsát és az innen kiinduló

3

lapbeli átló végpontjait. Az (1) alatti kocka esetében megfelelő az a

4

csúcs, amelyre a koordináták összege páros szám, valamint az a

4

is, amelyre páratlan az összeg. A (2) példából pedig az a 4‐4 csúcs ad megoldást, amelyben a "

-

'' jelek száma páros, illetve páratlan.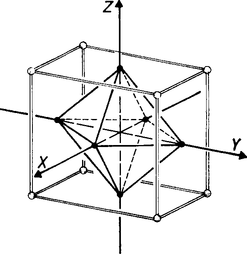

Szabályos oktaédert határoz meg a koordináta-rendszer

3

tengelyén az a

6

pont, mint csúcs, amelynek az origótól való távolsága

1.

Ezek konvex burkának minden lapja nyilvánvalóan szabályos háromszög. Más szóval: ezt az oktaédert határozzák meg a (2) kocka lapjainak középpontjai.
A szabályos dodekaéderre és a szabályos ikozaéderre együtt mutatjuk meg, hogy a kívánt elhelyezés nem lehetséges. A dodekaéder lapjai ugyanis szabályos ötszögek, az ikozaédernél pedig az egy csúcsból kiinduló öt él végpontjai adják egy szabályos ötszög csúcsait, így elég azt bebizonyítanunk, hogy szabályos ötszög nem helyezhető el úgy a térben (azaz nem valamelyik koordinátasíkon), hogy mindegyik csúcsának mindegyik koordinátája egész szám legyen. Sőt, elegendő ezt az ötszög három egymás utáni csúcsára belátni.
Legyenek ezek

A

B

és

C

úgy, hogy

A B = A C,

így

B A C ∢ = 108^{\circ},

és tegyük fel, hogy ‐ állításunkkal ellentétben ‐ az

A B C

háromszög csúcsai rácspontok. Ekkor a koordinátákból az ismert távolságképlettel számítva

A B^{2}

A C^{2}

és

B C^{2}

egyaránt egész számok, továbbá a

B C

oldalra felírt koszinusztétel alapján

\begin{matrix} cos^{2} 108^{\circ} = \frac{{(A B^{2} + A C^{2} - B C^{2})}^{2}}{4 A B^{2} \cdot A C^{2}}, \end{matrix}

racionális szám. Ez pedig ellentmondás, hiszen ismeretes, hogy

cos 108^{\circ} = - cos 72^{\circ} = - \frac{\sqrt[]{5} - 1}{4},

amiből

cos^{2} 108^{\circ} = \frac{3 - \sqrt[]{5}}{8},

tehát irracionális. Ezzel bebizonyítottuk állításunkat.

Megjegyzések. 1. Nagyobb élhosszúságot megengedve, a kocka nemcsak a bemutatott egyszerű (tréfásan: "kincstári'') módokon állítható be a koordinátarácsba. Legyen az

a

oldalú rácsnégyzet

A

csúcsa az origó, a vele szomszédos

B

és

D

csúcsok helyvektora

b (b_{1}, b_{2}, b_{3}),

illetve

d (d_{1}, d_{2}, d_{3}),

vagyis

\begin{matrix} b_{1}^{2} + b_{2}^{2} + b_{3}^{2} = a^{2}, d_{1}^{2} + d_{2}^{2} + d_{3}^{2} = a^{2}, b_{1} d_{1} + b_{2} d_{2} + b_{3} d_{3} = 0, \end{matrix}

tehát a négyzet negyedik csúcsa a

b+d

vektor

C

végpontja. Ilyen pontpár

a = 3

esetén

B (2, 2, 1)

és

D (- 2, 1, 2),

tehát

C (0, 3, 3) .

Most idézzük az 1982. évi Kürschák József Emlékverseny 1. feladatát: "Adott a térben egy egész oldalhosszúságú kocka, amelyről tudjuk, hogy az egyik lapján levő négy csúcs koordinátái valamennyien egész számok. Bizonyítandó, hogy a másik négy csúcs koordinátái is egész számok''. A megoldásban (Surányi János cikke, K. M. L. 1983. évi februári szám, 50. oldal) olvashatjuk, hogy ekkor ‐ tovább is itteni jelöléseinket használva ‐ az origóból kiinduló harmadik kockaél végpontjainak koordinátái: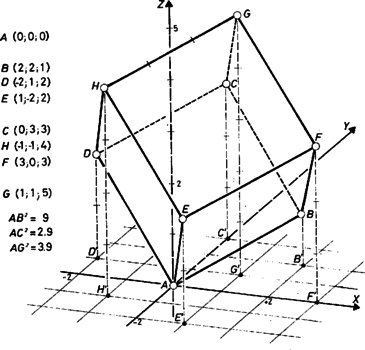

\begin{matrix} \frac{b_{2} d_{3} - b_{3} d_{2}}{a}, \frac{b_{3} d_{1} - b_{1} d_{3}}{a}, \frac{b_{1} d_{2} - b_{2} d_{1}}{a}, \end{matrix}

vagy ezek ellentettjei, valamint hogy e kifejezések egész számok. ‐ Példánkban az

A

-ból kiinduló harmadik kockaél végpontja

(1, - 2, 2)

‐ vagy pedig

(- 1, 2, - 2)

‐, ennek alapján a hátralevő három kockacsúcs koordinátái is felírhatók. (Lásd a borító 4. oldaláról idehelyezett ábrát!)

Kétszeresére nagyítva ezt a kockát, a lapközéppontok meghatározta szabályos oktaéderre is kapunk "általános'' elhelyezést.

2. Sokan észreveszik a példában az

1, 2, 2, 3

pitagoraszi "számnégyest'', valamint hogy a

D

csúcs egyike annak a

24

elemű pontegyüttesnek, amelyet

B

-ből kapunk, egyrészt permutálva a koordináták abszolút értékeit (

3

eset), másrészt eléjük illesztve a kétféle előjel ismétléses variációit (

24

rácspont bármely rácspont körüli,

a = 3

sugarú gömb felszínén; visszatérve

0 = A

-hoz, megkaphatjuk őket

B

-nek a koordinátasíkokon, valamint páronként vett szögfelezősíkjaikon való tükrözésekkel is).
Mégsem minden térbeli pitagoraszi számnégyes alkalmas ilyen példa felírására. Például

a = 21

esetén a

B (4, 8, 19)

ponthoz

47

további pont kapcsolható a megfelelő gömb felületén, de azok egyike sincs

90^{\circ}

-nyi szögtávolságban

B

-től. Ha azonban hozzávesszük azt a

4 \cdot 48 + 1 \cdot 24 = 216

pontot, amelyek a következőkből származtathatók :

\begin{matrix} 21^{2} = 4^{2} + 5^{2} + 20^{2} = 4^{2} + 13^{2} + 16^{2} = 6^{2} + 9^{2} + 18^{2} = 7^{2} + 14^{2} + 14^{2} = 8^{2} + 11^{2} + 16^{2}, \end{matrix}

e felbontások alapján számos új rácskockát írhatunk fel, például

19 (- 8) + 8 \cdot 11 + 4 \cdot 16 = 0

-ból.
B. T.

3. Az 1986. évi decemberi számunkban ‐ ezzel a feladattal egyidőben ‐ egy cikk jelent meg arról, hogy milyen szabályos rács-sokszögek léteznek a síkon Láttuk, hogy ha

n = 5

vagy

n > 6,

akkor nincs a síkon olyan szabályos

n

-szög, amelynek minden csúcsa rácspont. Az a bizonyítás szóról szóra átvihető térben (azaz nem valamelyik koordinátasíkon) elhelyezkedő szabályos

n

-szögekre (Megjegyezzük, hogy a bizonyításból csak azért zártuk ki az

n = 6

esetet, mert akkor az ottani

B

pontok egybeesnének; egyébként ezt az esetet már nyilván elintéztük a szabályos háromszöggel együtt.)
Mondhatjuk tehát, hogy a (3-dimenziós) térben valamivel változatosabb a helyzet; létezik szabályos rácsháromszög.
Csalódik azonban az, aki ezt a "terjeszkedést'' látva azt várja, hogy nagyobb dimenziós térben talán majd a szabályos ötszög csúcsai is ráilleszthetők rácspontokra. A fenti bizonyítás minden

n ≧ 2

dimenziós térre érvényes. (Abba már nem bocsátkozhatunk bele, mire gondoljunk az "

n

dimenziós tér'' kifejezés hallatára.)
B. Z.‐B. T.