| Feladat: | F.2612 | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Baboss Cs. , Beke T. , Benczúr A. , Bereczky Á. , Biró J. , Cynolter G. , Dienes J. , Eckert B. , Gyuris V. , Hajdú G. , Hajnal Z. , Kántor A. , Kecskés K. , Keleti T. , Kincses Z. , Kiss 303 B. , Kiss 969 Cs. , Klug R. , Lipták 182 L. , Lozsi I. , Majoros L. , Pál G. , Pfening A. , Pongor G. , Rimányi R. , Sass B. , Szabó 182 T. , Szabó 484 P. , Szalay Gy. , Talata I. , Tasnády P. , Veres E. , Wiandt T. , Zaránd G. | ||
| Füzet: | 1987/szeptember, 258 - 259. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Geometriai egyenlőtlenségek, Paralelepipedon, Súlyvonal, Köréírt alakzatok, Terület, felszín, Térfogat, Tetraéderek, Koszinusztétel alkalmazása, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1986/december: F.2612 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük az hosszúságú él végpontjait -val és -vel, a másikéit és -vel, a felezőpontok legyenek és . Használjuk az ábra egyéb jelöléseit is. 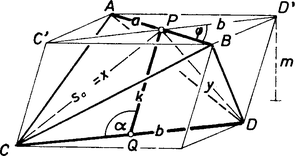 Szerkesszük meg a tetraéder köré írt paralelepipedont, vagyis azt a testet, amelyet a tetraéder kitérő élpárjaira illesztett párhuzamos síkok határolnak. E paralelepipedon egyik lapjának átlója az szakasz, és ennek a lapnak a másik átlója hosszúságú. Ezért a lap területe . Jelöljük a tetraéder térfogatát -vel. Ismeretes, hogy a körülírt paralelepipedon térfogata háromszor akkora, mint a tetraéderé. Nyilvánvaló továbbá, hogy a paralelepipedon említett lapjához tartozó magassága ‐ jelöljük ezt -mel ‐, legfeljebb akkora lehet mint , azaz . Egyenlőség itt csak akkor állhat, ha merőleges a paralelepipedon -t, illetve -t tartalmazó lapjaira, és akkor -re és -re is merőleges. Ezek után a paralelepipedon térfogatát a következőképpen becsüljük: A felszín becsléséhez vegyük figyelembe, hogy a tetraédert két, az élre, és két, a élre illeszkedő háromszög határolja. Mivel egy háromszögben egy adott oldalhoz tartozó magasság hossza nem nagyobb, mint az ugyanahhoz az oldalhoz tartozó súlyvonal, a háromszög területe a szokásos jelölésekkel legfeljebb Jelöljük a tetraéder felszínét -val. Az előbbiek szerint ekkor
|