Feladat: F.2605 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bagyinszki P. ,  Bánkövi Johanna ,  Benczúr A. ,  Gács A. ,  Heckenberger I. ,  Máté Nóra ,  Sass B. ,  Szabó Péter [1984-1988] ,  Szepesi Zsuzsanna ,  Talata István 
Füzet: 1987/május, 201 - 203. oldal  PDF  |  MathML 
Témakör(ök): Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Magasságvonal, Terület, felszín, Háromszögek szerkesztése, Ellenpélda, mint megoldási módszer a matematikában, Feladat
Hivatkozás(ok):Feladatok: 1986/november: F.2605

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először azt bizonyítjuk, hogy ha a C-nél derékszög van, akkor teljesül az egyenlőség. Írjuk fel kétféleképpen a háromszög kétszeres területét: 2T=ab=mc. Itt négyzetre emelve, majd 1m2-et kifejezve s végül a Pitagorasz-tételt felhasználva valóban a kívánt egyenlőséget kapjuk.

1m2=c2a2b2=a2+b2a2b2=1b2+1a2.

 
 
1. ábra
 

A feladat állítása azonban csak akkor lenne igaz, ha megfordítva, az (1) egyenlőségből következne, hogy a háromszögben C-nél derékszög van. Erre azonban könnyű ellenpéldát találni: legyen az  ABC háromszögben C-nél derékszög, és legyen b<a. Ekkor az előbb bizonyítottak szerint 1m2=1a2+1b2. Ha az AC=b oldalt tükrözzük az m magasság egyenesére, akkor az A'C=b szakaszt kapjuk. Az így kapott BCA' háromszögben A'C=b,BC=a és A' az AB szakaszon van, tehát a C-ből induló magasság változatlan, továbbra is m hosszúságú. Az (1) egyenlőség tehát továbbra is fennáll, másrészt most A'-nél tompaszög van, a C-nél tehát hegyesszög, a feladat állítása így nem igaz.
 

II. megoldás. Legyenek az a, b, c oldalakkal szemközti szögek rendre α, β, γ. Az általánosság megszorítása nélkül feltehetjük, hogy α≦β. Ekkor nyilván α<90∘. Az (1) egyenlőség mindkét oldalát ab-vel végigszorozva az
am⋅bm=ab+ba
egyenlőséghez jutunk. Minden háromszögben igaz, hogy ma=sinβ,mb=sinα és ab=sinαsinβ, tehát az egyenlőség így is írható :
1sinα⋅1sinβ=sinαsinβ+sinβsinα.

Ha most mindkét oldalt megszorozzuk sinαsinβ-val, akkor az 1=sin2α+sin2β egyenlőséghez jutunk, ahonnan a sin2α+cos2α=1 azonosság felhasználásával a sin2β=cos2α egyenlőséget kapjuk. Minthogy 0<α<90∘,0<β<180∘,sinβ és cosα pozitív, tehát azt kapjuk, hogy sinβ=cosα. De cosα=sin(90∘-α), így sinβ=sin(90∘-α). Ebből pedig az következik, hogy vagy β=90∘-α, vagy β=180∘-(90∘-α)=90∘+α, azaz vagy α+β=90∘, vagy β-α=90∘.
Könnyű látni, hogy a 0<α<90∘,α≦β,0<β<180∘ feltételek mellett átalakításaink ekvivalensek voltak, tehát az (1) egyenlőség két esetben teljesül: ha α+β=90∘, tehát a C-nél derékszög van, vagy ha β-α=90∘. (Ekkor β tompaszög, tehát γ hegyesszög.) A feladat állítása tehát nem igaz, az egyenlőség teljesül pl. az α=γ=30∘,β=120∘-os háromszögre is.
 
III. megoldás. A feladatot egy szerkesztési feladatra vezetjük vissza. Adva van egy háromszög két oldala, a és b, továbbá tudjuk, hogy a C-ből induló m magasságra teljesül az (1) összefüggés. Szerkesszük meg a háromszöget!
(1) alapján m=aba2+b2 szerkeszthető. Ekkor ismerjük az ABC háromszög C-ből induló két oldalát, CB=a-t és CA=b-t, valamint a C-ből induló magasságát, m-et. Ekkor az ismert módon szerkeszthető a háromszög: a=CB, mint átfogó fölé szerkesztünk egy derékszögű háromszöget, amelynek egyik befogója m. Legyen ez a CBT háromszög és legyen CT=m. A BT egyenest a C körüli b=CA sugarú körrel elmetszve két pontot kapunk, A-t és A'-t. Ezek a metszéspontok valóban létrejönnek, hiszen m=aba2+b2 miatt b>m nyilván teljesül.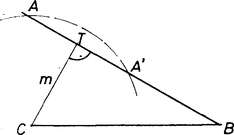
 
 
2. ábra
 

Ha a=b, akkor a metszéspontok egyike a B-vel esik egybe, minden más esetben két háromszöget kapunk: ABC-t és A'BC-t, és mindkettő megfelel. Világos az is, hogy a két háromszög közül csak az egyikben lehet a C-nél derékszög, hiszen ACB∢≠A'CB∢. Ezért a feladat állítása nem igaz: (1)-ből nem következik, hogy G-nél derékszög van.
 

Megjegyzések: 1. A harmadik megoldást az elsővel összevetve trigonometria alkalmazása nélkűl is könnyen láthatjuk, hogy (1) két esetben teljesül: ha α+β=90∘, vagy ha β-α=90∘.
2. Azokat a megoldásokat tekintettük kiemelkedőnek, amelyek a szögekre vonatkozó szükséges és elégséges feltételt adtak arra, hogy (1) teljesüljön, s ennek alapján mutatták meg, hogy a feladat állítása nem igaz. Voltak sajnos olyanok is, akik a trigonometrikus egyenletek megoldásánál nem ekvivalens átalakításokat hajtottak végre, ezeket akkor sem vettük kiemelkedőnek, ha végül véletlenül helyes eredményre jutottak.